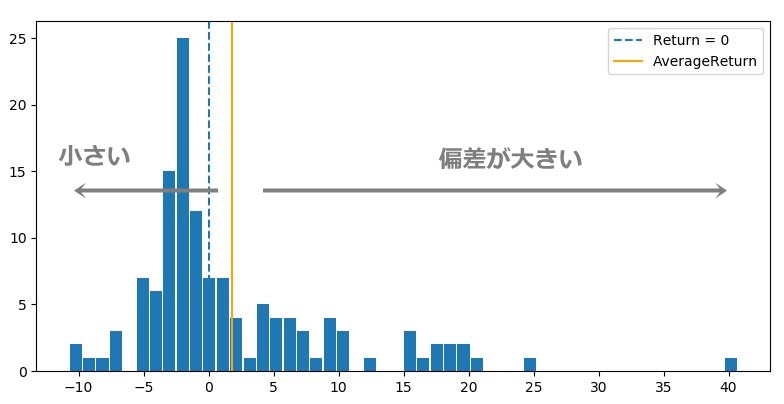
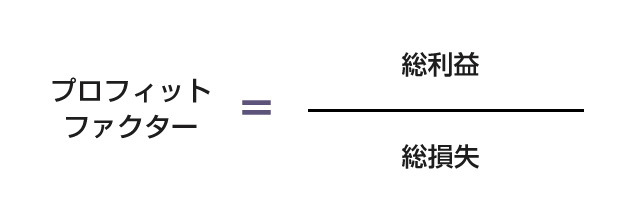
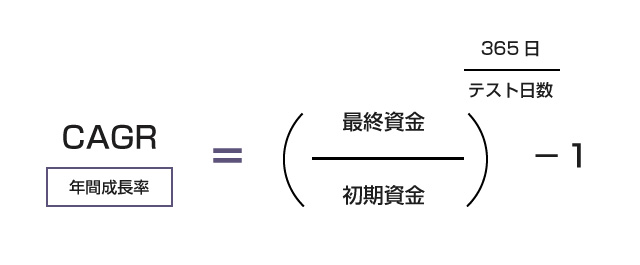
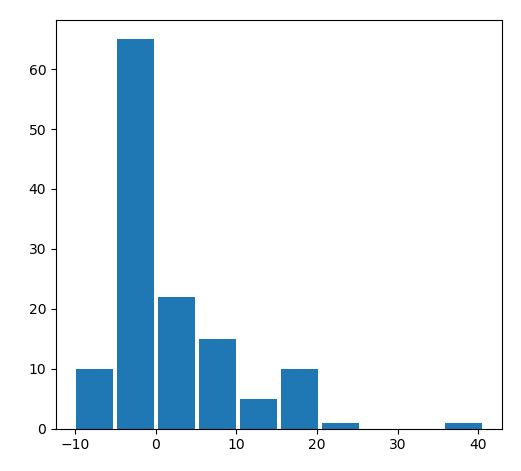
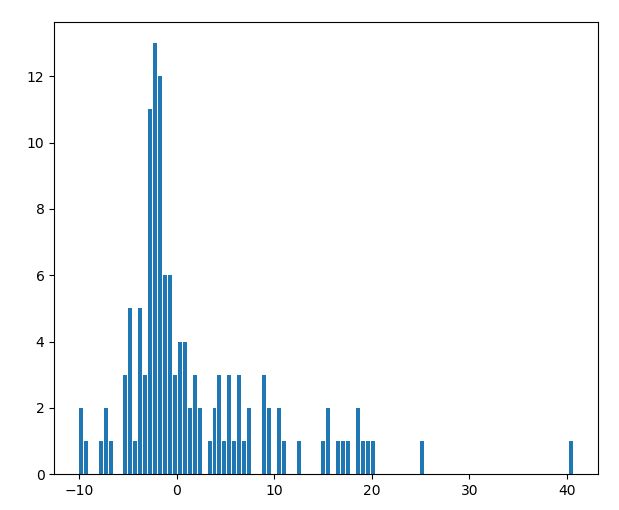
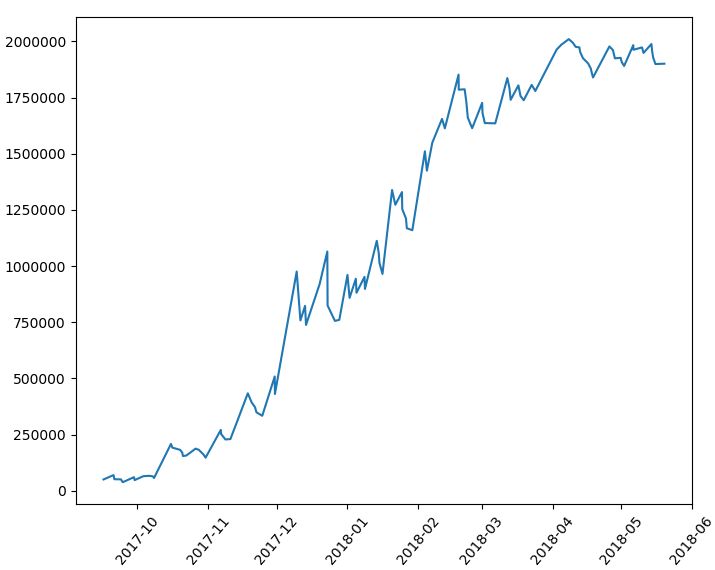
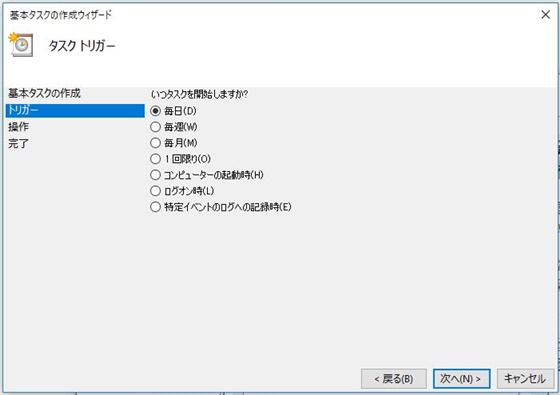
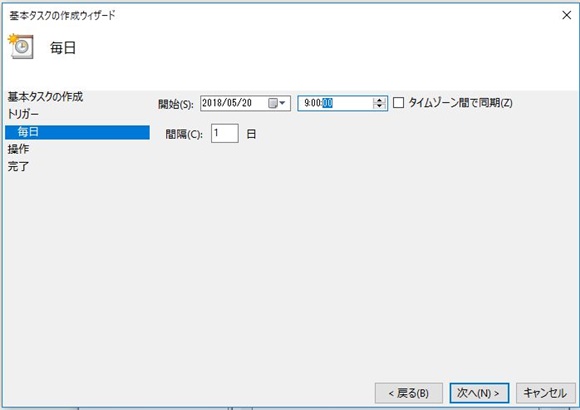
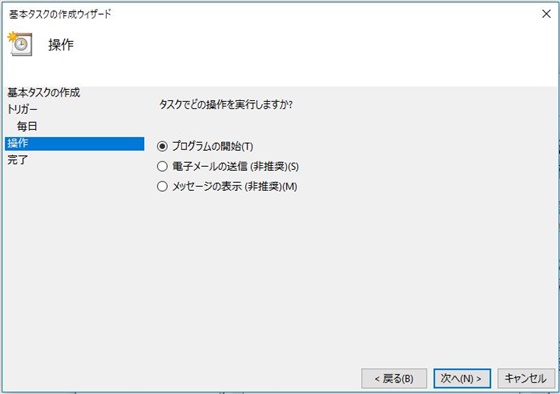
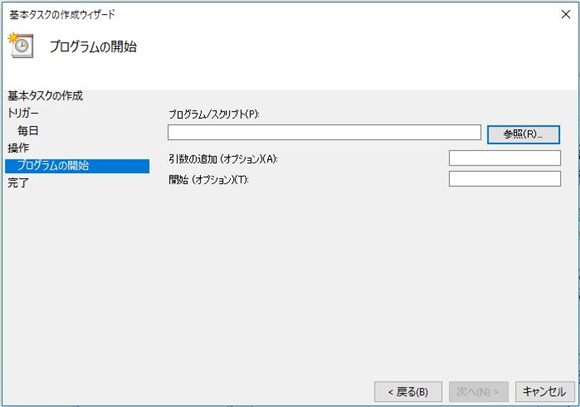
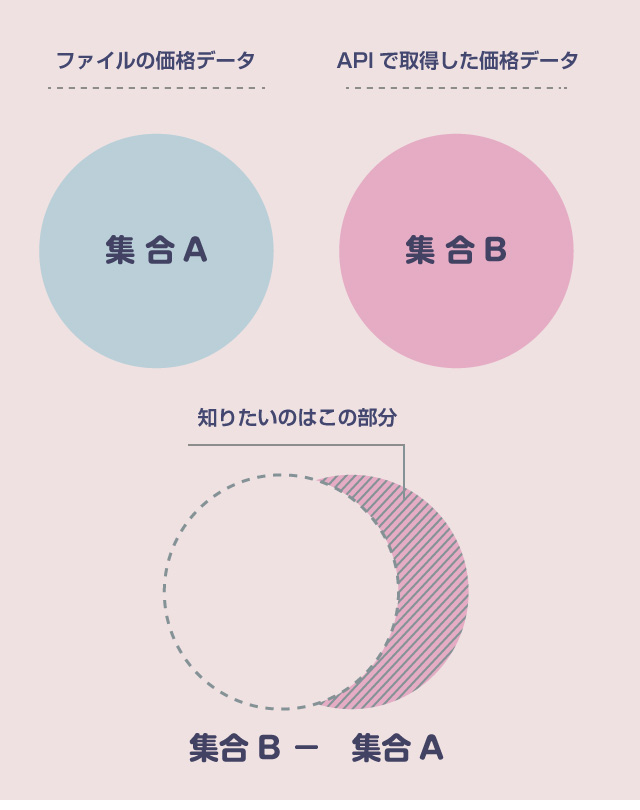
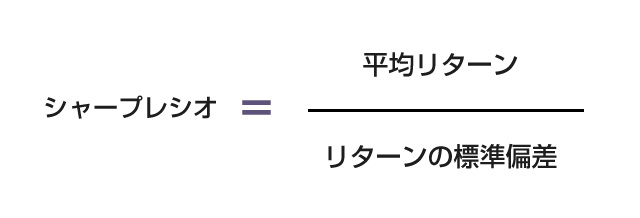さて、前回の記事では、チャネルブレイクアウトBOTの基本的な特徴としてリターンの分布が非対称であることと、なぜプラスの期待値が生まれるのかを相対度数表を使って確認しました。
今回の記事では、できるだけその特性を邪魔せずにエントリー精度を上げるための「フィルター」の追加について考えます。
フィルターの目的
ブレイクアウトBOTのようなトレンドフォロー型のBOTの場合、フィルターを追加する目的は主に以下の3つです。
(1)中長期のトレンドと方向性が一致しているか確認したい
(2)ブレイクアウトが本当に成功したかを確認したい
(3)ボラティリティの大きさや変動率を確認したい
他にも色々な目的のフィルターがあると思いますが、ここではおおまかな主目的をこの3つに絞ることにします。では具体的な例をみてみましょう。
トレンドの方向性を確認するフィルター
これは全体のトレンドと逆行する方向へのブレイクアウトを取り除くためのフィルターです。例えば、30期間の上値をブレイクアウトした場合、中長期でのトレンドが上向きかどうかを確認し、上向きと判断できた場合のみエントリーします。
いわゆるトレンドフィルターのことですが、これにも、シンプルなものから複雑なものまでいくつかバリエーションがあります。
買いのトレンドフィルターの例
1)現在の終値がn足前の終値の水準より高ければOK
2)現在の終値が長期移動平均線より上にあればOK
3)中期移動平均線が、前回の足より直近の足の方が上ならOK
4)現在の短期移動平均線が長期移動平均線より上にあればOK
いずれのフィルターも要するに、何らかの方法で全体の相場が中長期で上向きであることを確認しているに過ぎません。
「売買ルールはシンプルであればあるほど堅牢性があっていい」という信念のある方は、1)や2)のフィルターをより好むでしょう。一方、ある程度しっかり最適化することを好む方は、より変数の調整が可能な3)や4)のフィルターを好むでしょう。
フィルターを検証してみよう!
ではまずは検証条件を確認しておきましょう。前回までと同じ1時間足の30期間ドンチアン・チャネルブレイクアウトBOTで、全トレードは1BTCだけを売買するものとします。ストップは有効にします。
検証条件
・検証期間(2017/9/16~2018/5/25)
・1時間足を使用
・上値・下値ブレイクアウト 30期間
・ブレイクアウトの判定 高値/安値
・ボラティリティ計算期間 30期間
・ストップレンジ幅 2ATR
・トレイリングストップ 有効
・全トレードで1BTCだけを売買
フィルター無しの場合
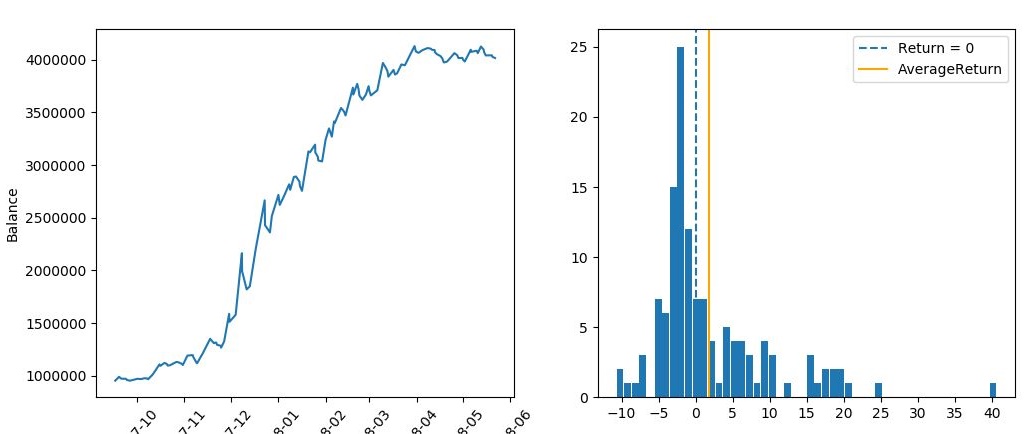
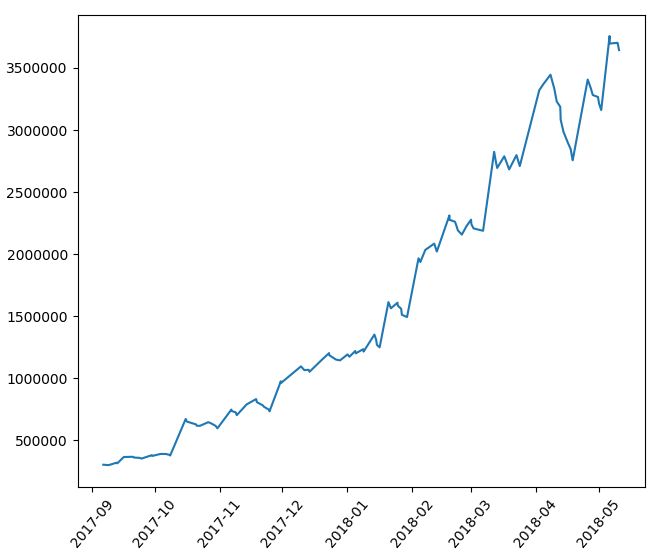
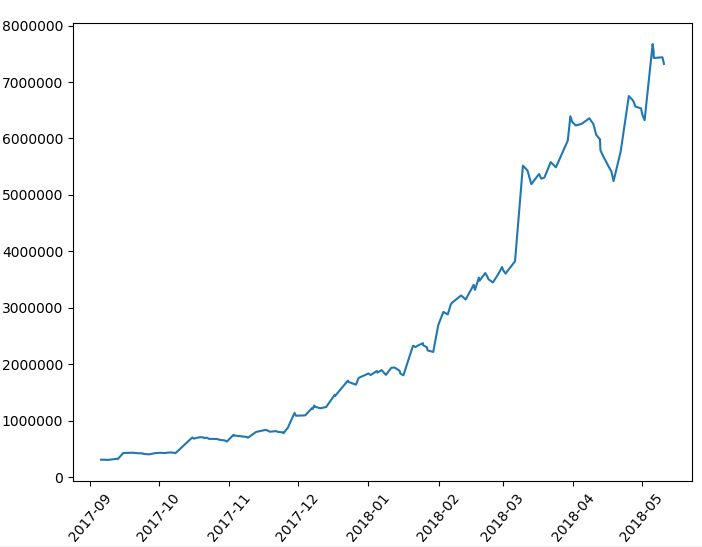
まずは比較対照となる「フィルターを使わなかった場合」の成績を確認しておきます。
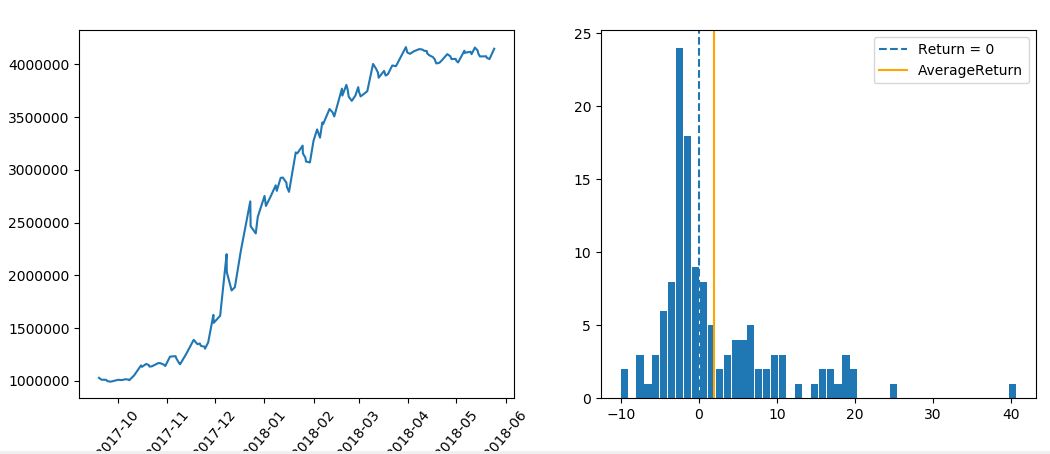
----------------------------------- 総合の成績 ----------------------------------- 全トレード数 : 129回 勝率 : 42.6% 平均リターン : 1.98% 標準偏差 : 7.74% 平均利益率 : 8.48% 平均損失率 : -2.86% 平均保有期間 : 31.7足分 損切りの回数 : 111回 最大の勝ちトレード : 584043円 最大の負けトレード : -235479円 最大連敗回数 : 10回 最大ドローダウン : -343866円 / -15.6% 利益合計 : 5693956円 損失合計 : -2544463円 最終損益 : 3149493円 初期資金 : 1000000円 最終資金 : 4149493円 運用成績 : 415.0% ----------------------------------- 各成績指標 ----------------------------------- CAGR(年間成長率) : 698.5% MARレシオ : 20.19 シャープレシオ : 0.26 プロフィットファクター : 2.24 損益レシオ : 2.97 ------------------------------------------ +10%を超えるトレードの回数 : 18回 ------------------------------------------ -10%を下回るトレードの回数 : 1回 ------------------------------------------
このリターン分布やトレード回数、勝率、期待値、プロフィットファクターなどの成績指標が、フィルターの適用でどう変化するのかを見ていきましょう!
1.「終値の水準が200期間前より上(下)」のフィルターを検証
まずは200期間を使った1つ目のフィルターをかけてみましょう。
1時間足の買いエントリーなら「現在の終値の水準が200時間前(約1週間前)の終値の水準より高い」ことをフィルター条件とし、売りエントリーなら逆に、現在の終値が200時間前の終値の水準より低いことをフィルター条件とします。
Pythonコード
詳しいロジックはあとで解説しますが、簡単にいうと、ブレイクアウトを判定する関数を呼んだあとに、エントリー(ドテン含む)のときだけ以下のようなフィルター判定の関数を実行します。手仕舞いの判定時にはフィルターをかけないので注意してください。
# エントリーフィルターの関数 def filter( signal ): if len(last_data) < 200: return True if data["close_price"] > last_data[-200]["close_price"] and signal["side"] == "BUY": return True if data["close_price"] < last_data[-200]["close_price"] and signal["side"] == "SELL": return True return False
なお、バックテストでは最初の200期間はフィルターチェックができないので無視しています。
検証結果
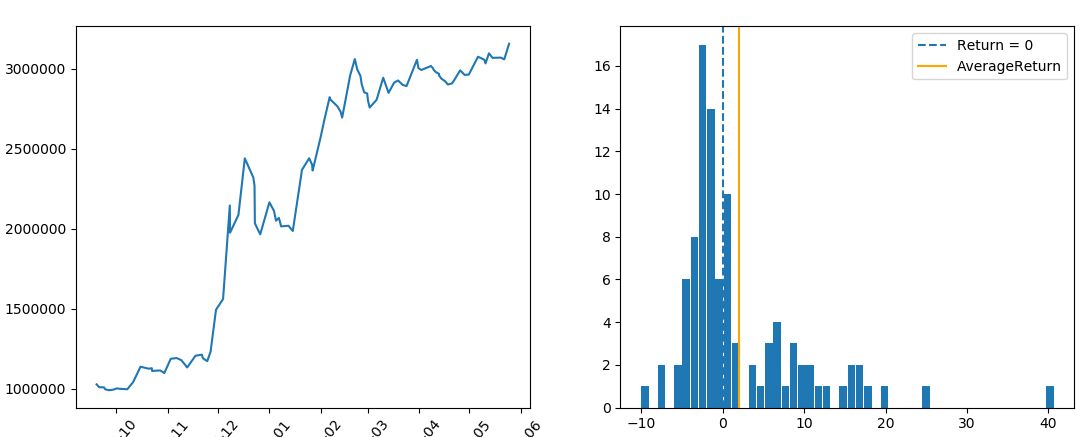
----------------------------------- 総合の成績 ----------------------------------- 全トレード数 : 98回 勝率 : 42.9% 平均リターン : 1.93% 標準偏差 : 7.77% 平均利益率 : 8.26% 平均損失率 : -2.82% 平均保有期間 : 29.7足分 損切りの回数 : 85回 最大の勝ちトレード : 584043円 最大の負けトレード : -235479円 最大連敗回数 : 8回 最大ドローダウン : -474261円 / -19.4% 利益合計 : 4111063円 損失合計 : -1956058円 最終損益 : 2155005円 初期資金 : 1000000円 最終資金 : 3155005円 運用成績 : 316.0% ----------------------------------- 各成績指標 ----------------------------------- CAGR(年間成長率) : 435.23% MARレシオ : 11.11 シャープレシオ : 0.25 プロフィットファクター : 2.1 損益レシオ : 2.93 ------------------------------------------ +10%を超えるトレードの回数 : 14回 ------------------------------------------ -10%を下回るトレードの回数 : 1回 ------------------------------------------
比較
| フィルター無し | フィルター有り | |
|---|---|---|
| トレード回数 | 129回 | 98回 |
| 勝率 | 42.6% | 42.9% |
| 期待値 | 1.98% | 1.93% |
| 最大DD | -15.6% | -19.4% |
| CAGR | 698.5% | 435.2% |
| MARレシオ | 20.19 | 11.11 |
| PF | 2.24 | 2.1 |
| 損益レシオ | 2.97 | 2.93 |
このフィルターは単にトレード回数を削っているだけで、ほとんど意味がありませんね。リターン分布の形状も変わっておらず、単に利益の出るトレード機会と損失の出るトレード機会をランダムに削ってしまっただけに見えます。
次にいきましょう。
2.「終値が200期間の単純移動平均より上(下)」のフィルターを検証
次に終値が200期間の単純移動平均(200MA)より上にあることを買いフィルターの条件とし、その逆を売りフィルターの条件としてみましょう。
Pythonコード
エントリーフィルターの関数は以下のように書きました。前回の記事で作成した移動平均線を計算する関数(calculate_MA())を使っています。
# エントリーフィルターの関数 def filter( signal ): if len(last_data) < 200: return True if data["close_price"] > calculate_MA(200) and signal["side"] == "BUY": return True if data["close_price"] < calculate_MA(200) and signal["side"] == "SELL": return True return False
検証結果
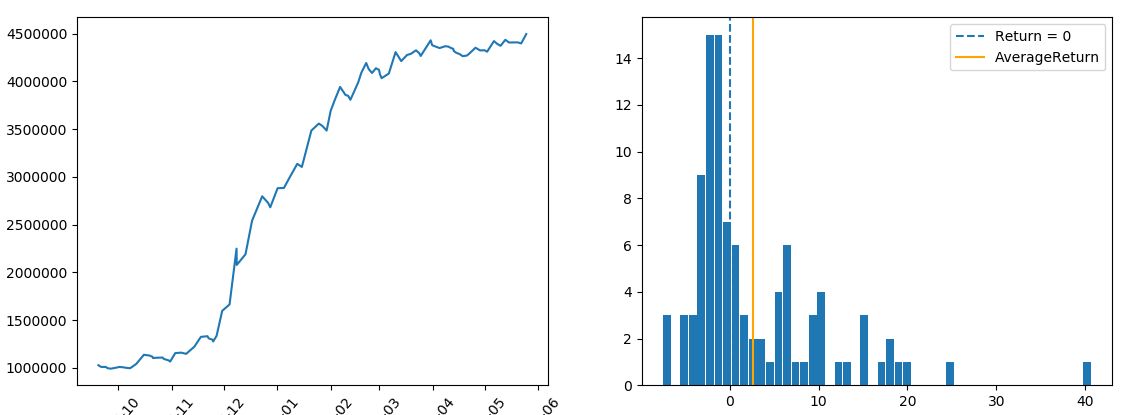
----------------------------------- 総合の成績 ----------------------------------- 全トレード数 : 100回 勝率 : 47.0% 平均リターン : 2.65% 標準偏差 : 7.8% 平均利益率 : 8.49% 平均損失率 : -2.53% 平均保有期間 : 32.9足分 損切りの回数 : 86回 最大の勝ちトレード : 584043円 最大の負けトレード : -170307円 最大連敗回数 : 8回 最大ドローダウン : -170307円 / -7.6% 利益合計 : 4897309円 損失合計 : -1402143円 最終損益 : 3495166円 初期資金 : 1000000円 最終資金 : 4495166円 運用成績 : 450.0% ----------------------------------- 各成績指標 ----------------------------------- CAGR(年間成長率) : 797.45% MARレシオ : 45.99 シャープレシオ : 0.34 プロフィットファクター : 3.49 損益レシオ : 3.36 ------------------------------------------ +10%を超えるトレードの回数 : 16回 ------------------------------------------ -10%を下回るトレードの回数 : 0回 ------------------------------------------
比較
| フィルター無し | フィルター有り | |
|---|---|---|
| トレード回数 | 129回 | 100回 |
| 勝率 | 42.6% | 47.0% |
| 期待値 | 1.98% | 2.65% |
| 最大DD | -15.6% | -7.6% |
| CAGR | 698.5% | 797.45% |
| MARレシオ | 20.19 | 45.99 |
| PF | 2.24 | 3.49 |
| 損益レシオ | 2.97 | 3.36 |
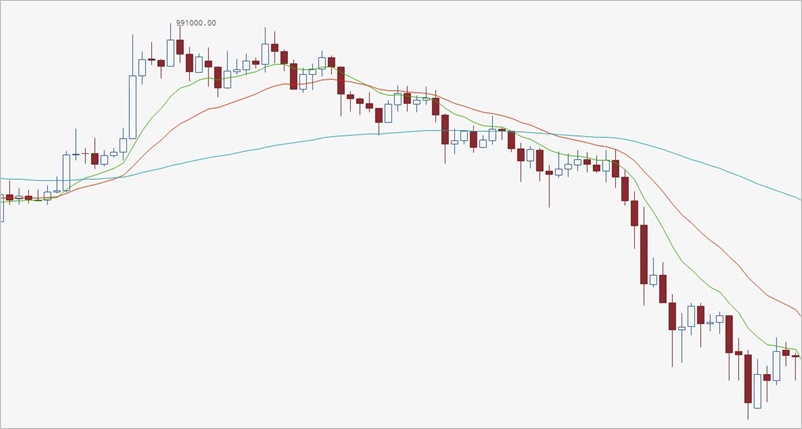
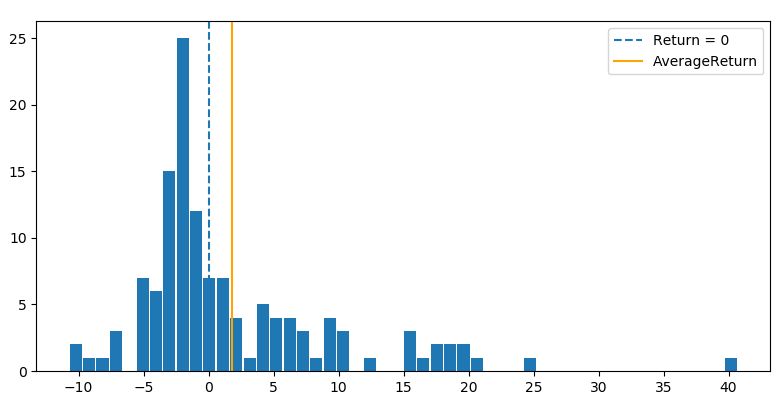
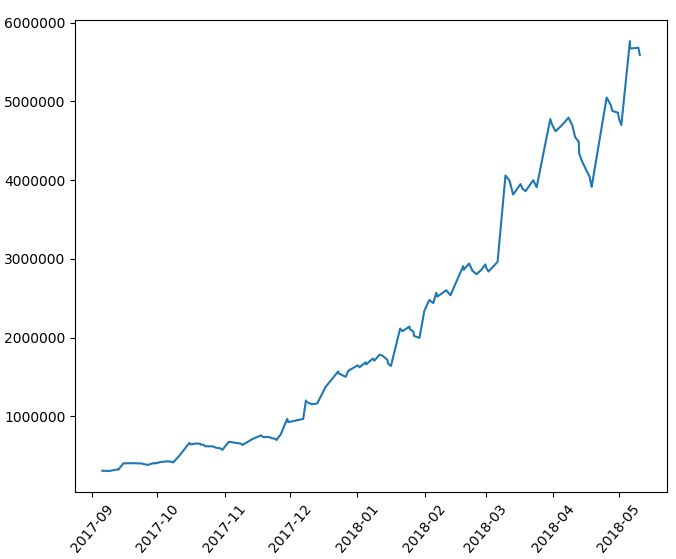
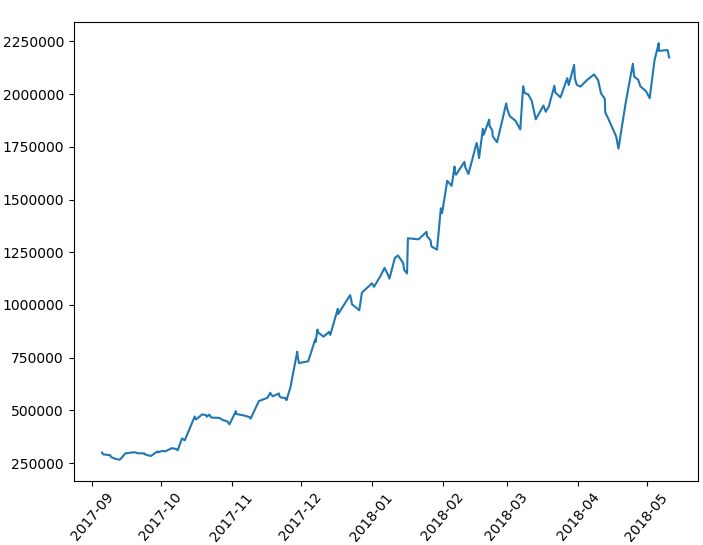
同じ200期間を使ったフィルターでも、こちらの方が遥かに優秀なフィルターとして機能しています。リターン分布を見ると、-3%台に多く分布していた損失がかなりフィルターにかけられているのがわかります。
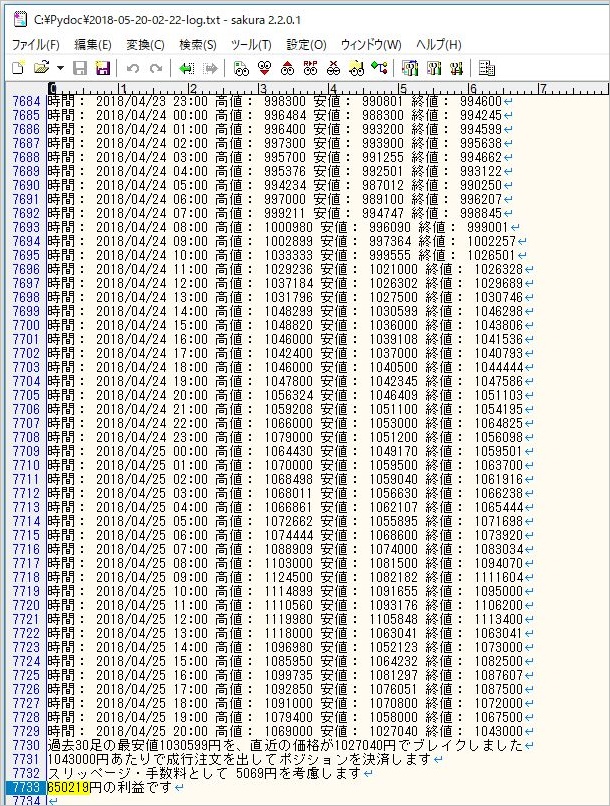
では、このフィルターが機能したのは具体的にどのような場面なのでしょうか? ログから直近のチャートでフィルターにかかった箇所を確認してみましょう。
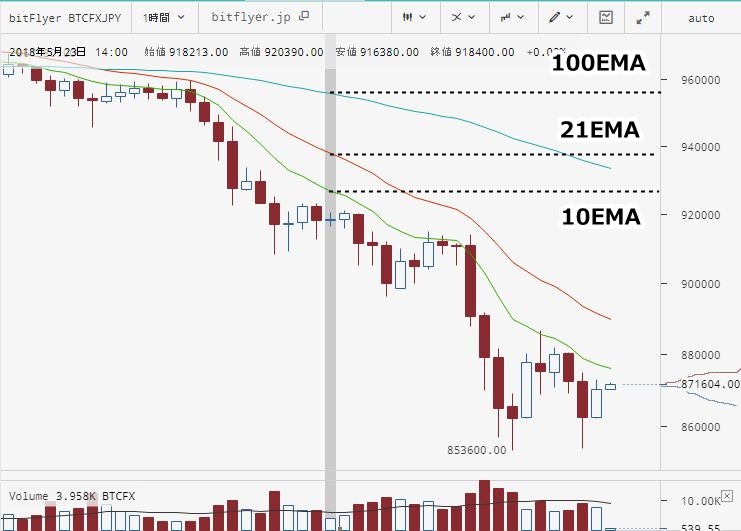
▽ 5月19日22時の確定足
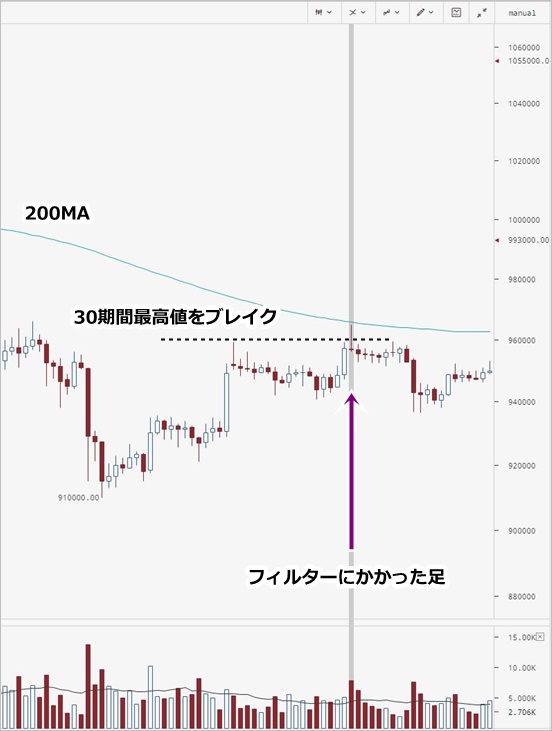
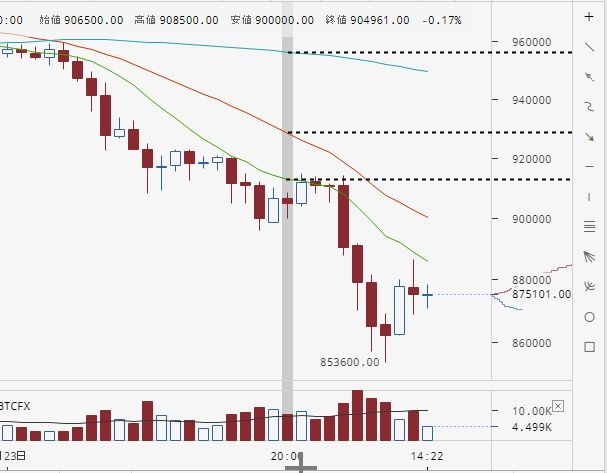
全体として下落相場が続くなか、1時間足が30期間の最高値をブレイクアウトしたものの、終値が200期間単純移動平均より下にあるため、エントリーを見送っていたことがわかります。
3.「20期間移動平均の数値が前回の足よりも直近の足で上(下)」のフィルターを検証
これも簡易的なトレンドの判定方法の1つです。「終値の20期間移動平均線が前足よりも直近の足のほうが高い」ことを買いフィルターの条件とし、その逆を売りフィルターの条件とします。
これは要するに、移動平均線の「傾き」を簡易的にチェックする方法です。移動平均線の向きはそう簡単に変わりませんので、直近の足とその1つ前の足を比較すれば、現在の向き(傾き)がわかります。
参考情報
この判定方法は、ラリーウィリアムズ氏が「短期売買法」という本の中で、ボラティリティブレイクアウトについて解説している箇所(4章)で紹介した方法です。以下そのまま引用してみます。
市場が上昇トレンドにあるときだけトレードするというのはどうだろう。良い考えだが、上昇トレンドであることをどう見極めればよいのだろうか。私が好んで用いる方法のひとつは、終値の20日移動平均線が前日よりも今日のほうが高いときを上昇トレンドとする、というものだ。(略)。ボラティリティブレイクアウト戦略を市場が上昇トレンドにあるときのみ使った結果を見ると、その成果は絶大であることが分かる。
143項より
どの期間の移動平均線を使うかは(200MAのような明かな長期線を除き)かなり主観的な問題になるので、カーブフィッティングに繋がりやすくなります。そのため、判断が難しいところなのですが、ここでは、この本のまま20期間移動平均を使うことにします。
▽ 検証結果
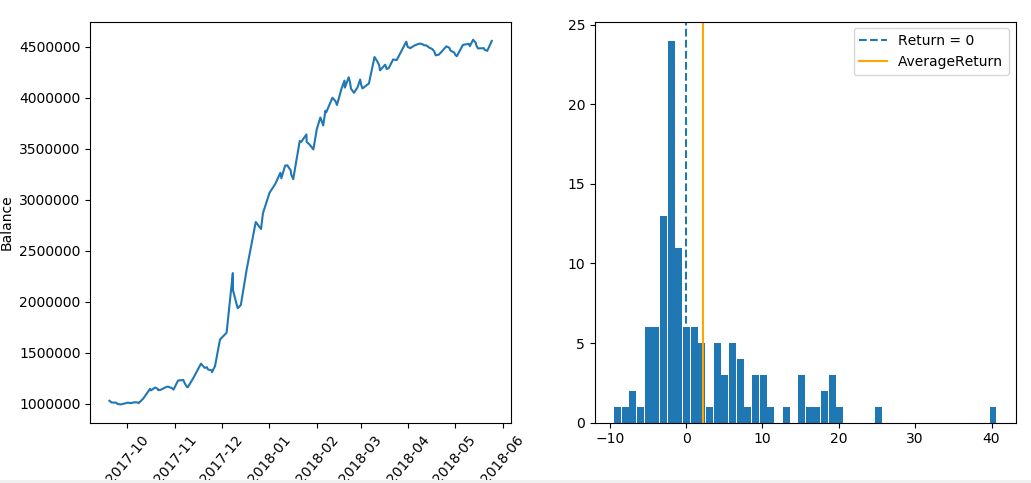
----------------------------------- 総合の成績 ----------------------------------- 全トレード数 : 122回 勝率 : 44.3% 平均リターン : 2.27% 標準偏差 : 7.78% 平均利益率 : 8.58% 平均損失率 : -2.74% 平均保有期間 : 32.9足分 損切りの回数 : 105回 最大の勝ちトレード : 584043円 最大の負けトレード : -173559円 最大連敗回数 : 8回 最大ドローダウン : -343866円 / -15.1% 利益合計 : 5659592円 損失合計 : -2102250円 最終損益 : 3557342円 初期資金 : 1000000円 最終資金 : 4557342円 運用成績 : 456.0% ----------------------------------- 各成績指標 ----------------------------------- CAGR(年間成長率) : 815.63% MARレシオ : 23.56 シャープレシオ : 0.29 プロフィットファクター : 2.69 損益レシオ : 3.13 ------------------------------------------ +10%を超えるトレードの回数 : 18回 ------------------------------------------ -10%を下回るトレードの回数 : 0回 ------------------------------------------
比較
| フィルター無し | フィルター有り | |
|---|---|---|
| トレード回数 | 129回 | 122回 |
| 勝率 | 42.6% | 44.3% |
| 期待値 | 1.98% | 2.27% |
| 最大DD | -15.6% | -15.1% |
| CAGR | 698.5% | 815.63% |
| MARレシオ | 20.19 | 23.56 |
| PF | 2.24 | 2.69 |
| 損益レシオ | 2.97 | 3.13 |
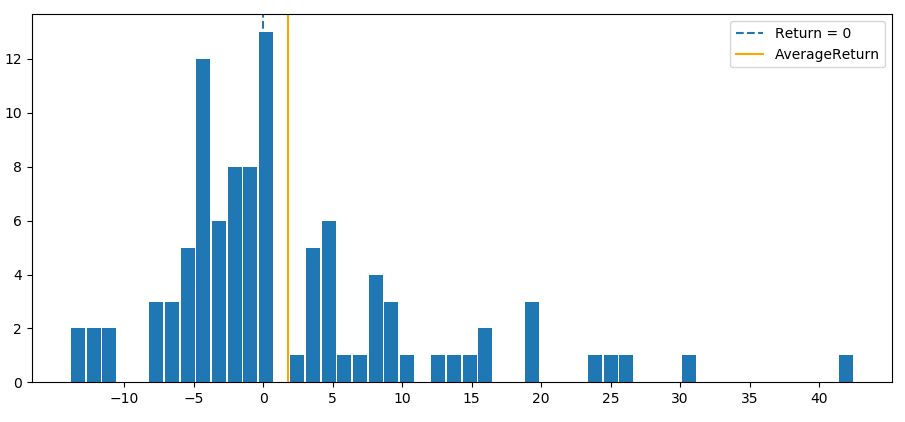
今までのフィルターの中では、最も緩いフィルターですね。全てのエントリー機会(129回)のうち、フィルターにかけたのは7回分だけです。一方で成績はかなり改善しており、10%を超えるトレード機会は1度も逃していません。
ただ、このデータだけだと「たまたま一番悪い損失が外れただけ」の可能性もあるので注意が必要です。一応、さきほどと同じように直近のチャートから実際の場面を確認しておきましょう。
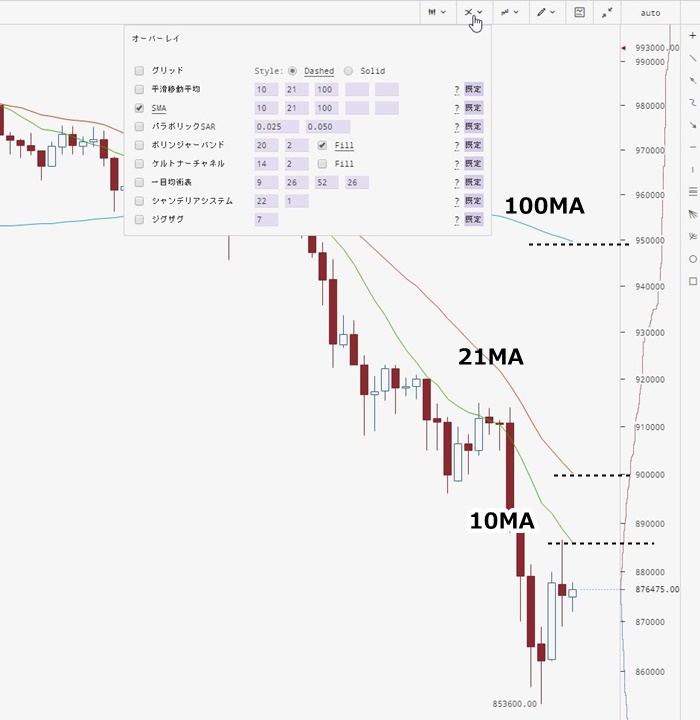
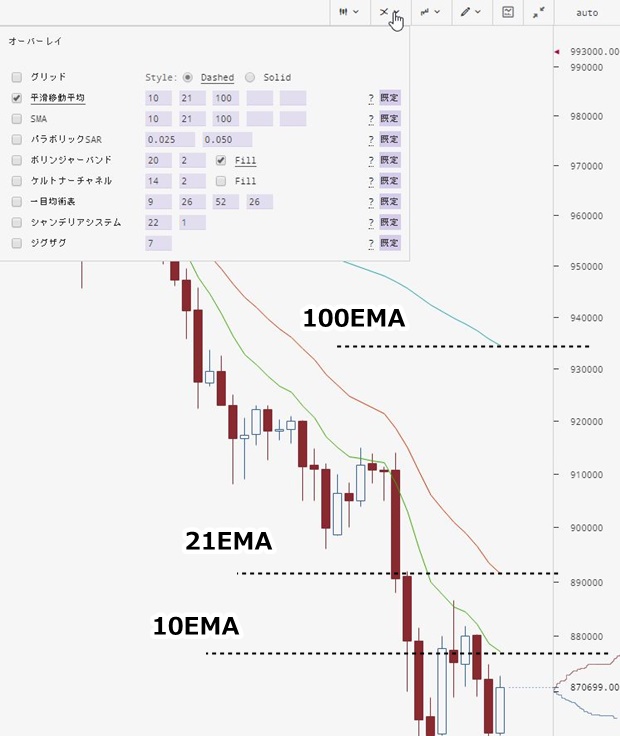
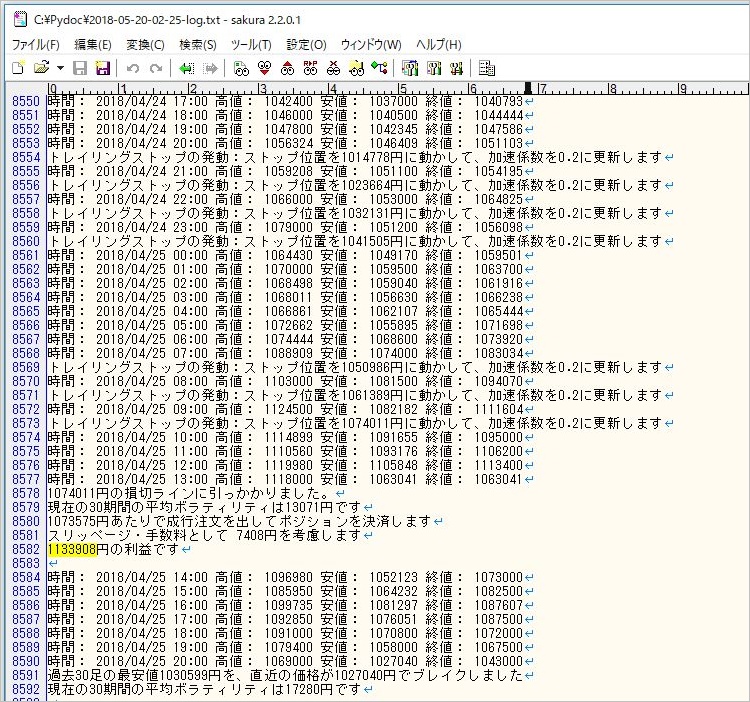
ログを見ると直近では5月6日7時の確定足がフィルターにかかっています。以下の場面ですね。
▽ 5月6日7時の確定足
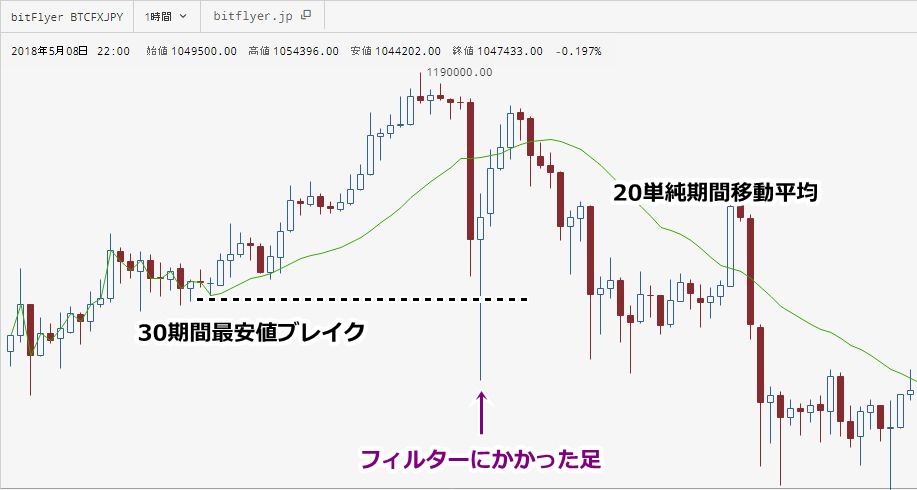
最安値がブレイクアウトしたものの、20期間移動平均がまだ上向きのため、エントリーを見送っています。
Pythonコード
# エントリーフィルターの関数 def filter( signal ): if len(last_data) < 20: return True if calculate_MA(20) > calculate_MA(20,-1) and signal["side"] == "BUY": return True if calculate_MA(20) < calculate_MA(20,-1) and signal["side"] == "SELL": return True return False
4.「短期移動平均線が長期移動平均線よりも上(下)」のフィルターを検証
最後はもっとも複雑なフィルターです。
例えば、買いエントリーであれば、短期移動平均線が長期移動平均線よりも上にある場合にのみエントリーします。売りエントリーであれば、短期移動平均線が長期移動平均線よりも下にある場合のみエントリーします。
このフィルターを使うためには、「どの期間の移動平均線を使うか?」という点で、最低でも2つ恣意的な数値(変数)を決めなければなりません。
そのため、好みが分かれそうな手法ですが、チャネルブレイクアウトのバイブル的な存在の本「タートル流 投資の魔術」で、トレンドフィルターとして紹介されているので、こちらも紹介しておきます。
使用する移動平均線
本家では、「350日指数移動平均と25日指数移動平均線」とされていますので、ここでもそのまま350EMAと25EMAを使うことにします。ただし本家のタートル流チャネルブレイクアウトは、30期間ブレイクアウトではないので前提条件は少し違います。
▽ 検証結果
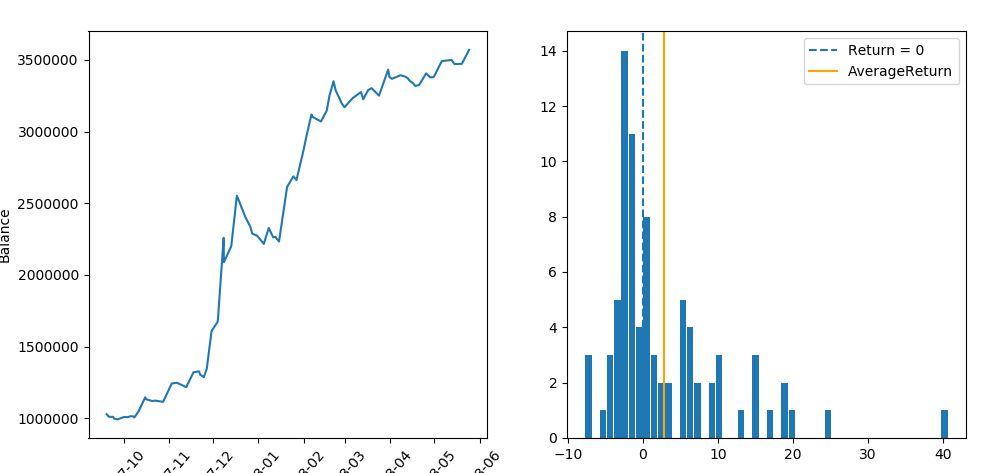
----------------------------------- 総合の成績 ----------------------------------- 全トレード数 : 82回 勝率 : 50.0% 平均リターン : 2.76% 標準偏差 : 8.1% 平均利益率 : 8.19% 平均損失率 : -2.67% 平均保有期間 : 33.4足分 損切りの回数 : 71回 最大の勝ちトレード : 584043円 最大の負けトレード : -170307円 最大連敗回数 : 5回 最大ドローダウン : -336319円 / -13.2% 利益合計 : 3884653円 損失合計 : -1313956円 最終損益 : 2570697円 初期資金 : 1000000円 最終資金 : 3570697円 運用成績 : 357.0% ----------------------------------- 各成績指標 ----------------------------------- CAGR(年間成長率) : 541.24% MARレシオ : 19.47 シャープレシオ : 0.34 プロフィットファクター : 2.96 損益レシオ : 3.07 ------------------------------------------ +10%を超えるトレードの回数 : 13回 ------------------------------------------ -10%を下回るトレードの回数 : 0回 ------------------------------------------
比較
| フィルター無し | フィルター有り | |
|---|---|---|
| トレード回数 | 129回 | 82回 |
| 勝率 | 42.6% | 50.0% |
| 期待値 | 1.98% | 2.76% |
| 最大DD | -15.6% | -13.2% |
| CAGR | 698.5% | 541.24% |
| MARレシオ | 20.19 | 19.47 |
| PF | 2.24 | 2.96 |
| 損益レシオ | 2.97 | 3.07 |
今まで見てきたトレンドフィルターの中では、最もアクティブ(攻撃的)なフィルターです。全129回のトレード機会のうち、49回(およそ1/3)をフィルターにかけてエントリー機会を絞っています。
その結果、勝率は50%、期待値は2.76%、プロフィットファクターは2.96と、個別のトレードの質(成績)はかなり向上しています。しかしトレード回数がかなり減ってしまったため、運用成績(CAGR)は悪化しています。
Pythonコード
# エントリーフィルターの関数 def filter( signal ): if len(last_data) < 700: return True if calculate_EMA(350) < calculate_EMA(25) and signal["side"] == "BUY": return True if calculate_EMA(350) > calculate_EMA(25) and signal["side"] == "SELL": return True return False
指数平滑移動平均(EMA)の計算には、こちらの記事の関数を使っています。
トレンドフィルターの意味
なお、ここまで敢えてわかりやすく「エントリー機会を絞る」と表現してきましたが、もう少し正確にトレンドフィルターを使うことの意味を、チャートやログで確認しておきましょう。
トレンドフォロー型のBOTの基本的なコンセプトは、将来の価格を予測するのではなく、単にブレイクアウトした方向に事後的に追従するというものです。そのため、勝率はともかくとしてトレンドが発生すればそれに乗ることは保証されます。
一方、ここに移動平均線を用いたトレンドフィルターを加えるということは、本質的には「トレンドとの一致を確認するまでエントリーを保留する」ことを意味します。
具体的なケース(1)
例えば、2番目の「現在の終値が200MAより上(下)」のフィルターを使った場合を見てみましょう。ログから直近の2018年5月7日のBitflyerFXの1時間足のチャートを確認してみます。
以下の場面です。
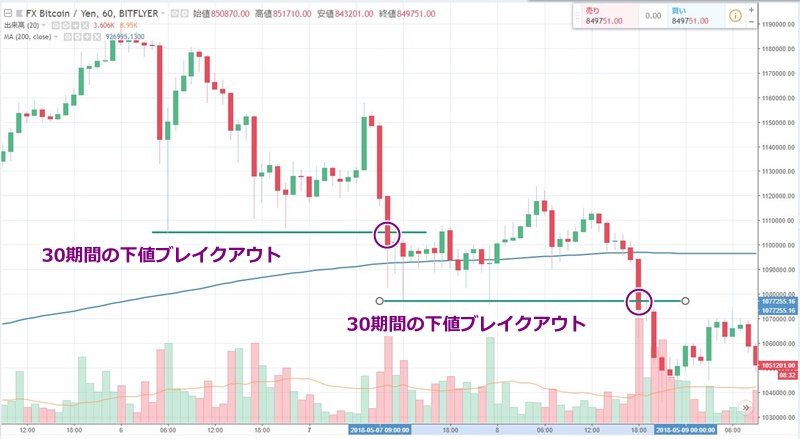
※ ブレイクアウトの判定基準が「終値」の場合
この場面では、最初に30期間の最安値をブレイクアウトして売りシグナルが出ていますが、「終値が200MAより上にある」という理由でエントリーを見送っています。
しかし「30期間の下値ブレイクアウト」のシグナルは、その後も、最安値を更新するたびに出続けます。そして次のシグナルでは「終値が200MAより下にある」ため、フィルター条件と一致し、結局、エントリーは成立しています。
このように移動平均線は価格の遅行指標なので、ブレイクアウトが本当にトレンドを伴うものであれば、そのうち必ずエントリーシグナルとフィルター条件は一致します。これが「トレンドを確認するまでエントリーを保留する」といった意味です。
具体的なケース(2)
もちろん上記の役割だけだと、単にトレンドに乗り遅れるだけでメリットがありません。しかしこのフィルターの役割がさらに有効に機能する場面があります。
例えば、以下は先ほどと同じ「現在の終値が200MAより上(下)」フィルターを使った場合の、2018年5月16日のチャートの場面です。
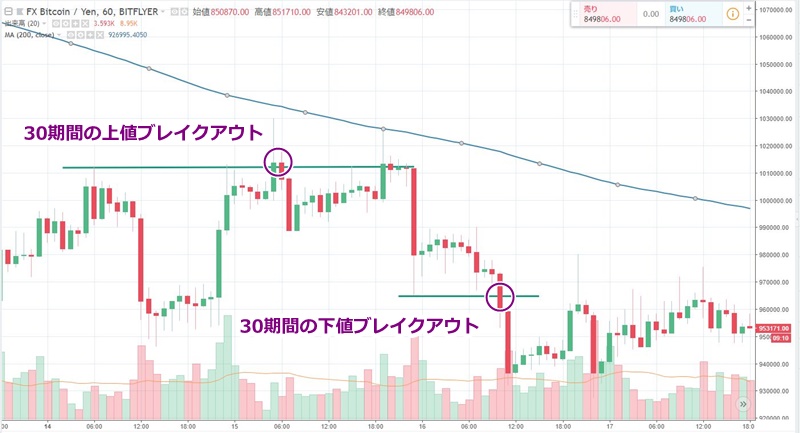
ここでは1度目の「30期間の最高値ブレイクアウト」を、終値が200MAより下にあるという理由で見送っています。
もしこのブレイクアウトがトレンドの転換を伴うのであれば、その後、終値は200MAを超えていくはずです。しかし価格は下落を続け、今度は「30期間の最安値」をブレイクアウトしました。今度は、終値が200MAより下にあるため、エントリーの条件を満たしています。
結果、無駄な最高値ブレイクアウトによる買いエントリーを1つ減らすことができました。
まとめ
このようにトレンドフィルターを付けるということの本質的な意味は、「トレンド指標とブレイクアウトの方向が一致していなければ、トレンド指標が追従してくるまでエントリーを保留する」という点にあります。
そう理解しておけば、メリットとデメリットも把握できます。フィルターが強すぎるとエントリーが遅れて参入エッジが無くなる一方、適切なフィルターを用いると、「トレンドを伴わないブレイクアウト」に参加して損切りにかかる回数を減らすことができます。
フィルター条件を追加するpythonコード
それでは、最後にPythonでフィルターをつける方法を解説しましょう。
まず今回作成したフィルターは、以下のようなかたちで関数にしておきます。
# 設定値 filter_VER = "A" # OFFでフィルター無効 # エントリーフィルターの関数 def filter( signal ): if filter_VER == "OFF": return True if filter_VER == "A": if len(last_data) < 200: return True if data["close_price"] > last_data[-200]["close_price"] and signal["side"] == "BUY": return True if data["close_price"] < last_data[-200]["close_price"] and signal["side"] == "SELL": return True if filter_VER == "B": if len(last_data) < 200: return True if data["close_price"] > calculate_MA(200) and signal["side"] == "BUY": return True if data["close_price"] < calculate_MA(200) and signal["side"] == "SELL": return True if filter_VER == "C": if len(last_data) < 20: return True if calculate_MA(20) > calculate_MA(20,-1) and signal["side"] == "BUY": return True if calculate_MA(20) < calculate_MA(20,-1) and signal["side"] == "SELL": return True if filter_VER == "D": if len(last_data) < 700: return True if calculate_EMA(350) < calculate_EMA(25) and signal["side"] == "BUY": return True if calculate_EMA(350) > calculate_EMA(25) and signal["side"] == "SELL": return True return False
このフィルター関数は、今まで作成していた「エントリー条件を判定する関数」とセットで使います。
エントリー条件の判定関数が、買いか売りかのシグナル(signal)を返す設計になっているので、そのsignalをそのまま渡します。フィルター条件を満たしていればTrueを返し、フィルター条件を満たさなければFalseを返します。もちろんTrueが返ってきた場合のみエントリーします。
そのため、以下のようにエントリー関数も修正します。
エントリー注文を出す関数
# エントリー注文を出す関数
def entry_signal( data,last_data,flag ):
signal = donchian( data,last_data )
if signal["side"] == "BUY":
flag["records"]["log"].append("過去{0}足の最高値{1}円を、直近の価格が{2}円でブレイクしました\n".format(buy_term,signal["price"],data[judge_price["BUY"]]))
# フィルター条件を確認
if filter( signal ) == False:
flag["records"]["log"].append("フィルターのエントリー条件を満たさなかったため、エントリーしません\n")
return flag
# 以下同じ
フィルター条件の判定を「ブレイクアウトを判定する関数」の中に入れてしまっても構いません。ただしその場合は、手仕舞いのときに間違ってフィルターがかからないように条件分岐が必要です。
▽ フィルター適用の注意点
(1)30期間の上値ブレイクアウトで買いエントリー
⇒ フィルターが必要
(2)エントリー後、30期間の下値ブレイクアウトで手仕舞い
⇒ フィルターは不要
(3)さらにそのままドテンして売りエントリー
⇒ フィルターが必要
BitflyerのEMAの注意点
なお、4つ目のフィルターの検証結果について、こちらも実際にBitflyerのチャートと照らし合わせて確認したかったのですが、350EMAのズレが大きかったので断念しました。
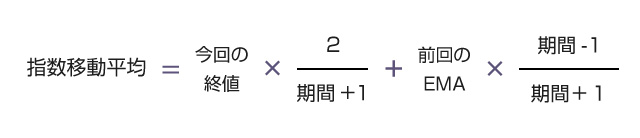
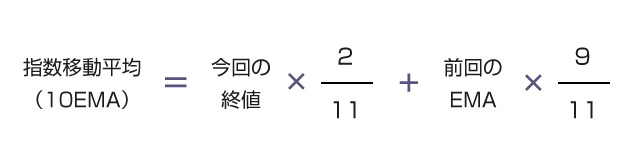
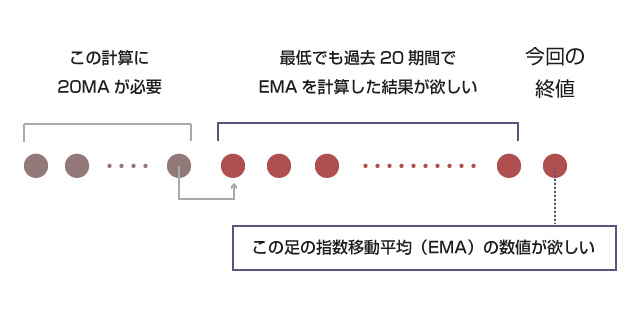
指数移動平滑平均(EMA)は「誰が計算しても1つの値に定まる」という性質の数値ではありません。どれだけの過去データを考慮に入れるかによって数値が変動します。そのため、売買シグナルにBitflyerのチャート画面に表示されるのと同じEMAの数値を使いたい場合は注意が必要です。
詳しくは前回の記事で解説しているので参考にしてください。
今回勉強したコード
最後に今回使ったコードを記載しておきます。
次回は、「ブレイクアウトに成功したことを確認するフィルター」について考察します。
import requests
from datetime import datetime
import time
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
#--------設定項目--------
chart_sec = 3600 # 1時間足を使用
buy_term = 30 # 買いエントリーのブレイク期間の設定
sell_term = 30 # 売りエントリーのブレイク期間の設定
judge_price={
"BUY" : "high_price", # ブレイク判断 高値(high_price)か終値(close_price)を使用
"SELL": "low_price" # ブレイク判断 安値 (low_price)か終値(close_price)を使用
}
TEST_MODE_LOT = "fixed" # fixed なら常に1BTC固定 / adjustable なら可変ロット
volatility_term = 30 # 平均ボラティリティの計算に使う期間
stop_range = 2 # 何レンジ幅にストップを入れるか
trade_risk = 0.03 # 1トレードあたり口座の何%まで損失を許容するか
levarage = 3 # レバレッジ倍率の設定
start_funds = 1000000 # シミュレーション時の初期資金
entry_times = 2 # 何回に分けて追加ポジションを取るか
entry_range = 1 # 何レンジごとに追加ポジションを取るか
stop_config = "TRAILING" # ON / OFF / TRAILING の3つが設定可
stop_AF = 0.02 # 加速係数
stop_AF_add = 0.02 # 加速係数を増やす度合
stop_AF_max = 0.2 # 加速係数の上限
filter_VER = "A" # OFFで無効
wait = 0 # ループの待機時間
slippage = 0.001 # 手数料・スリッページ
#-------------補助ツールの関数--------------
# CryptowatchのAPIを使用する関数
def get_price(min, before=0, after=0):
price = []
params = {"periods" : min }
if before != 0:
params["before"] = before
if after != 0:
params["after"] = after
response = requests.get("https://api.cryptowat.ch/markets/bitflyer/btcfxjpy/ohlc",params)
data = response.json()
if data["result"][str(min)] is not None:
for i in data["result"][str(min)]:
if i[1] != 0 and i[2] != 0 and i[3] != 0 and i[4] != 0:
price.append({ "close_time" : i[0],
"close_time_dt" : datetime.fromtimestamp(i[0]).strftime('%Y/%m/%d %H:%M'),
"open_price" : i[1],
"high_price" : i[2],
"low_price" : i[3],
"close_price": i[4] })
return price
else:
flag["records"]["log"].append("データが存在しません")
return None
# 時間と高値・安値をログに記録する関数
def log_price( data,flag ):
log = "時間: " + datetime.fromtimestamp(data["close_time"]).strftime('%Y/%m/%d %H:%M') + " 高値: " + str(data["high_price"]) + " 安値: " + str(data["low_price"]) + " 終値: " + str(data["close_price"]) + "\n"
flag["records"]["log"].append(log)
return flag
# 平均ボラティリティを計算する関数
def calculate_volatility( last_data ):
high_sum = sum(i["high_price"] for i in last_data[-1 * volatility_term :])
low_sum = sum(i["low_price"] for i in last_data[-1 * volatility_term :])
volatility = round((high_sum - low_sum) / volatility_term)
flag["records"]["log"].append("現在の{0}期間の平均ボラティリティは{1}円です\n".format( volatility_term, volatility ))
return volatility
# 単純移動平均を計算する関数
def calculate_MA( value,before=None ):
if before is None:
MA = sum(i["close_price"] for i in last_data[-1*value:]) / value
else:
MA = sum(i["close_price"] for i in last_data[-1*value + before: before]) / value
return round(MA)
# 指数移動平均を計算する関数
def calculate_EMA( value,before=None ):
if before is not None:
MA = sum(i["close_price"] for i in last_data[-2*value + before : -1*value + before]) / value
EMA = (last_data[-1*value + before]["close_price"] * 2 / (value+1)) + (MA * (value-1) / (value+1))
for i in range(value-1):
EMA = (last_data[-1*value+before+1 + i]["close_price"] * 2 /(value+1)) + (EMA * (value-1) / (value+1))
else:
MA = sum(i["close_price"] for i in last_data[-2*value: -1*value]) / value
EMA = (last_data[-1*value]["close_price"] * 2 / (value+1)) + (MA * (value-1) / (value+1))
for i in range(value-1):
EMA = (last_data[-1*value+1 + i]["close_price"] * 2 /(value+1)) + (EMA * (value-1) / (value+1))
return round(EMA)
#-------------エントリーフィルターの関数--------------
# エントリーフィルターの関数
def filter( signal ):
if filter_VER == "OFF":
return True
if filter_VER == "A":
if len(last_data) < 200:
return True
if data["close_price"] > last_data[-200]["close_price"] and signal["side"] == "BUY":
return True
if data["close_price"] < last_data[-200]["close_price"] and signal["side"] == "SELL":
return True
if filter_VER == "B":
if len(last_data) < 200:
return True
if data["close_price"] > calculate_MA(200) and signal["side"] == "BUY":
return True
if data["close_price"] < calculate_MA(200) and signal["side"] == "SELL":
return True
if filter_VER == "C":
if len(last_data) < 20:
return True
if calculate_MA(20) > calculate_MA(20,-1) and signal["side"] == "BUY":
return True
if calculate_MA(20) < calculate_MA(20,-1) and signal["side"] == "SELL":
return True
if filter_VER == "D":
if len(last_data) < 400:
return True
if calculate_EMA(200) < calculate_EMA(14) and signal["side"] == "BUY":
return True
if calculate_EMA(200) > calculate_EMA(14) and signal["side"] == "SELL":
return True
return False
#-------------資金管理の関数--------------
# 注文ロットを計算する関数
def calculate_lot( last_data,data,flag ):
# 固定ロットでのテスト時
if TEST_MODE_LOT == "fixed":
flag["records"]["log"].append("固定ロット(1枚)でテスト中のため、1BTCを注文します\n")
lot = 1
volatility = calculate_volatility( last_data )
stop = stop_range * volatility
flag["position"]["ATR"] = round( volatility )
return lot,stop,flag
# 口座残高を取得する
balance = flag["records"]["funds"]
# 最初のエントリーの場合
if flag["add-position"]["count"] == 0:
# 1回の注文単位(ロット数)と、追加ポジの基準レンジを計算する
volatility = calculate_volatility( last_data )
stop = stop_range * volatility
calc_lot = np.floor( balance * trade_risk / stop * 100 ) / 100
flag["add-position"]["unit-size"] = np.floor( calc_lot / entry_times * 100 ) / 100
flag["add-position"]["unit-range"] = round( volatility * entry_range )
flag["add-position"]["stop"] = stop
flag["position"]["ATR"] = round( volatility )
flag["records"]["log"].append("\n現在のアカウント残高は{}円です\n".format( balance ))
flag["records"]["log"].append("許容リスクから購入できる枚数は最大{}BTCまでです\n".format( calc_lot ))
flag["records"]["log"].append("{0}回に分けて{1}BTCずつ注文します\n".format( entry_times, flag["add-position"]["unit-size"] ))
# 2回目以降のエントリーの場合
else:
balance = round( balance - flag["position"]["price"] * flag["position"]["lot"] / levarage )
# ストップ幅には、最初のエントリー時に計算したボラティリティを使う
stop = flag["add-position"]["stop"]
# 実際に購入可能な枚数を計算する
able_lot = np.floor( balance * levarage / data["close_price"] * 100 ) / 100
lot = min(able_lot, flag["add-position"]["unit-size"])
flag["records"]["log"].append("証拠金から購入できる枚数は最大{}BTCまでです\n".format( able_lot ))
return lot,stop,flag
# 複数回に分けて追加ポジションを取る関数
def add_position( data,flag ):
# ポジションがない場合は何もしない
if flag["position"]["exist"] == False:
return flag
# 固定ロット(1BTC)でのテスト時は何もしない
if TEST_MODE_LOT == "fixed":
return flag
# 最初(1回目)のエントリー価格を記録
if flag["add-position"]["count"] == 0:
flag["add-position"]["first-entry-price"] = flag["position"]["price"]
flag["add-position"]["last-entry-price"] = flag["position"]["price"]
flag["add-position"]["count"] += 1
while True:
# 以下の場合は、追加ポジションを取らない
if flag["add-position"]["count"] >= entry_times:
return flag
# この関数の中で使う変数を用意
first_entry_price = flag["add-position"]["first-entry-price"]
last_entry_price = flag["add-position"]["last-entry-price"]
unit_range = flag["add-position"]["unit-range"]
current_price = data["close_price"]
# 価格がエントリー方向に基準レンジ分だけ進んだか判定する
should_add_position = False
if flag["position"]["side"] == "BUY" and (current_price - last_entry_price) > unit_range:
should_add_position = True
elif flag["position"]["side"] == "SELL" and (last_entry_price - current_price) > unit_range:
should_add_position = True
else:
break
# 基準レンジ分進んでいれば追加注文を出す
if should_add_position == True:
flag["records"]["log"].append("\n前回のエントリー価格{0}円からブレイクアウトの方向に{1}ATR({2}円)以上動きました\n".format( last_entry_price, entry_range, round( unit_range ) ))
flag["records"]["log"].append("{0}/{1}回目の追加注文を出します\n".format(flag["add-position"]["count"] + 1, entry_times))
# 注文サイズを計算
lot,stop,flag = calculate_lot( last_data,data,flag )
if lot < 0.01:
flag["records"]["log"].append("注文可能枚数{}が、最低注文単位に満たなかったので注文を見送ります\n".format(lot))
flag["add-position"]["count"] += 1
return flag
# 追加注文を出す
if flag["position"]["side"] == "BUY":
entry_price = first_entry_price + (flag["add-position"]["count"] * unit_range)
#entry_price = round((1 + slippage) * entry_price)
flag["records"]["log"].append("現在のポジションに追加して、{0}円で{1}BTCの買い注文を出します\n".format(entry_price,lot))
# ここに買い注文のコードを入れる
if flag["position"]["side"] == "SELL":
entry_price = first_entry_price - (flag["add-position"]["count"] * unit_range)
#entry_price = round((1 - slippage) * entry_price)
flag["records"]["log"].append("現在のポジションに追加して、{0}円で{1}BTCの売り注文を出します\n".format(entry_price,lot))
# ここに売り注文のコードを入れる
# ポジション全体の情報を更新する
flag["position"]["stop"] = stop
flag["position"]["price"] = int(round(( flag["position"]["price"] * flag["position"]["lot"] + entry_price * lot ) / ( flag["position"]["lot"] + lot )))
flag["position"]["lot"] = np.round( (flag["position"]["lot"] + lot) * 100 ) / 100
if flag["position"]["side"] == "BUY":
flag["records"]["log"].append("{0}円の位置にストップを更新します\n".format(flag["position"]["price"] - stop))
elif flag["position"]["side"] == "SELL":
flag["records"]["log"].append("{0}円の位置にストップを更新します\n".format(flag["position"]["price"] + stop))
flag["records"]["log"].append("現在のポジションの取得単価は{}円です\n".format(flag["position"]["price"]))
flag["records"]["log"].append("現在のポジションサイズは{}BTCです\n\n".format(flag["position"]["lot"]))
flag["add-position"]["count"] += 1
flag["add-position"]["last-entry-price"] = entry_price
return flag
# トレイリングストップの関数
def trail_stop( data,flag ):
# まだ追加ポジションの取得中であれば何もしない
if flag["add-position"]["count"] < entry_times and TEST_MODE_LOT != "fixed":
return flag
# 高値/安値がエントリー価格からいくら離れたか計算
if flag["position"]["side"] == "BUY":
moved_range = round( data["high_price"] - flag["position"]["price"] )
if flag["position"]["side"] == "SELL":
moved_range = round( flag["position"]["price"] - data["low_price"] )
# 最高値・最安値を更新したか調べる
if moved_range < 0 or flag["position"]["stop-EP"] >= moved_range:
return flag
else:
flag["position"]["stop-EP"] = moved_range
# 加速係数に応じて損切りラインを動かす
flag["position"]["stop"] = round(flag["position"]["stop"] - ( moved_range + flag["position"]["stop"] ) * flag["position"]["stop-AF"])
# 加速係数を更新
flag["position"]["stop-AF"] = round( flag["position"]["stop-AF"] + stop_AF_add ,2 )
if flag["position"]["stop-AF"] >= stop_AF_max:
flag["position"]["stop-AF"] = stop_AF_max
# ログ出力
if flag["position"]["side"] == "BUY":
flag["records"]["log"].append("トレイリングストップの発動:ストップ位置を{}円に動かして、加速係数を{}に更新します\n".format( round(flag["position"]["price"] - flag["position"]["stop"]) , flag["position"]["stop-AF"] ))
else:
flag["records"]["log"].append("トレイリングストップの発動:ストップ位置を{}円に動かして、加速係数を{}に更新します\n".format( round(flag["position"]["price"] + flag["position"]["stop"]) , flag["position"]["stop-AF"] ))
return flag
#-------------売買ロジックの部分の関数--------------
# ドンチャンブレイクを判定する関数
def donchian( data,last_data ):
highest = max(i["high_price"] for i in last_data[ (-1* buy_term): ])
if data[ judge_price["BUY"] ] > highest:
return {"side":"BUY","price":highest}
lowest = min(i["low_price"] for i in last_data[ (-1* sell_term): ])
if data[ judge_price["SELL"] ] < lowest:
return {"side":"SELL","price":lowest}
return {"side" : None , "price":0}
# エントリー注文を出す関数
def entry_signal( data,last_data,flag ):
signal = donchian( data,last_data )
if signal["side"] == "BUY":
flag["records"]["log"].append("過去{0}足の最高値{1}円を、直近の価格が{2}円でブレイクしました\n".format(buy_term,signal["price"],data[judge_price["BUY"]]))
# フィルター条件を確認
if filter( signal ) == False:
flag["records"]["log"].append("フィルターのエントリー条件を満たさなかったため、エントリーしません\n")
return flag
lot,stop,flag = calculate_lot( last_data,data,flag )
if lot > 0.01:
flag["records"]["log"].append("{0}円で{1}BTCの買い注文を出します\n".format(data["close_price"],lot))
# ここに買い注文のコードを入れる
flag["records"]["log"].append("{0}円にストップを入れます\n".format(data["close_price"] - stop))
flag["position"]["lot"],flag["position"]["stop"] = lot,stop
flag["position"]["exist"] = True
flag["position"]["side"] = "BUY"
flag["position"]["price"] = data["close_price"]
else:
flag["records"]["log"].append("注文可能枚数{}が、最低注文単位に満たなかったので注文を見送ります\n".format(lot))
if signal["side"] == "SELL":
flag["records"]["log"].append("過去{0}足の最安値{1}円を、直近の価格が{2}円でブレイクしました\n".format(sell_term,signal["price"],data[judge_price["SELL"]]))
# フィルター条件を確認
if filter( signal ) == False:
flag["records"]["log"].append("フィルターのエントリー条件を満たさなかったため、エントリーしません\n")
return flag
lot,stop,flag = calculate_lot( last_data,data,flag )
if lot > 0.01:
flag["records"]["log"].append("{0}円で{1}BTCの売り注文を出します\n".format(data["close_price"],lot))
# ここに売り注文のコードを入れる
flag["records"]["log"].append("{0}円にストップを入れます\n".format(data["close_price"] + stop))
flag["position"]["lot"],flag["position"]["stop"] = lot,stop
flag["position"]["exist"] = True
flag["position"]["side"] = "SELL"
flag["position"]["price"] = data["close_price"]
else:
flag["records"]["log"].append("注文可能枚数{}が、最低注文単位に満たなかったので注文を見送ります\n".format(lot))
return flag
# 手仕舞いのシグナルが出たら決済の成行注文 + ドテン注文 を出す関数
def close_position( data,last_data,flag ):
if flag["position"]["exist"] == False:
return flag
flag["position"]["count"] += 1
signal = donchian( data,last_data )
if flag["position"]["side"] == "BUY":
if signal["side"] == "SELL":
flag["records"]["log"].append("過去{0}足の最安値{1}円を、直近の価格が{2}円でブレイクしました\n".format(sell_term,signal["price"],data[judge_price["SELL"]]))
flag["records"]["log"].append(str(data["close_price"]) + "円あたりで成行注文を出してポジションを決済します\n")
# 決済の成行注文コードを入れる
records( flag,data,data["close_price"] )
flag["position"]["exist"] = False
flag["position"]["count"] = 0
flag["position"]["stop-AF"] = stop_AF
flag["position"]["stop-EP"] = 0
flag["add-position"]["count"] = 0
# ドテン注文の箇所
if filter( signal ) == False:
flag["records"]["log"].append("フィルターのエントリー条件を満たさなかったため、ドテンエントリーはしません\n")
return flag
lot,stop,flag = calculate_lot( last_data,data,flag )
if lot > 0.01:
flag["records"]["log"].append("\n{0}円で{1}BTCの売りの注文を入れてドテンします\n".format(data["close_price"],lot))
# ここに売り注文のコードを入れる
flag["records"]["log"].append("{0}円にストップを入れます\n".format(data["close_price"] + stop))
flag["position"]["lot"],flag["position"]["stop"] = lot,stop
flag["position"]["exist"] = True
flag["position"]["side"] = "SELL"
flag["position"]["price"] = data["close_price"]
if flag["position"]["side"] == "SELL":
if signal["side"] == "BUY":
flag["records"]["log"].append("過去{0}足の最高値{1}円を、直近の価格が{2}円でブレイクしました\n".format(buy_term,signal["price"],data[judge_price["BUY"]]))
flag["records"]["log"].append(str(data["close_price"]) + "円あたりで成行注文を出してポジションを決済します\n")
# 決済の成行注文コードを入れる
records( flag,data,data["close_price"] )
flag["position"]["exist"] = False
flag["position"]["count"] = 0
flag["position"]["stop-AF"] = stop_AF
flag["position"]["stop-EP"] = 0
flag["add-position"]["count"] = 0
# ドテン注文の箇所
if filter( signal ) == False:
flag["records"]["log"].append("フィルターのエントリー条件を満たさなかったため、ドテンエントリーはしません\n")
return flag
lot,stop,flag = calculate_lot( last_data,data,flag )
if lot > 0.01:
flag["records"]["log"].append("\n{0}円で{1}BTCの買いの注文を入れてドテンします\n".format(data["close_price"],lot))
# ここに買い注文のコードを入れる
flag["records"]["log"].append("{0}円にストップを入れます\n".format(data["close_price"] - stop))
flag["position"]["lot"],flag["position"]["stop"] = lot,stop
flag["position"]["exist"] = True
flag["position"]["side"] = "BUY"
flag["position"]["price"] = data["close_price"]
return flag
# 損切ラインにかかったら成行注文で決済する関数
def stop_position( data,flag ):
# トレイリングストップを実行
if stop_config == "TRAILING":
flag = trail_stop( data,flag )
if flag["position"]["side"] == "BUY":
stop_price = flag["position"]["price"] - flag["position"]["stop"]
if data["low_price"] < stop_price:
flag["records"]["log"].append("{0}円の損切ラインに引っかかりました。\n".format( stop_price ))
stop_price = round( stop_price - 2 * calculate_volatility(last_data) / ( chart_sec / 60) )
flag["records"]["log"].append(str(stop_price) + "円あたりで成行注文を出してポジションを決済します\n")
# 決済の成行注文コードを入れる
records( flag,data,stop_price,"STOP" )
flag["position"]["exist"] = False
flag["position"]["count"] = 0
flag["position"]["stop-AF"] = stop_AF
flag["position"]["stop-EP"] = 0
flag["add-position"]["count"] = 0
if flag["position"]["side"] == "SELL":
stop_price = flag["position"]["price"] + flag["position"]["stop"]
if data["high_price"] > stop_price:
flag["records"]["log"].append("{0}円の損切ラインに引っかかりました。\n".format( stop_price ))
stop_price = round( stop_price + 2 * calculate_volatility(last_data) / (chart_sec / 60) )
flag["records"]["log"].append(str(stop_price) + "円あたりで成行注文を出してポジションを決済します\n")
# 決済の成行注文コードを入れる
records( flag,data,stop_price,"STOP" )
flag["position"]["exist"] = False
flag["position"]["count"] = 0
flag["position"]["stop-AF"] = stop_AF
flag["position"]["stop-EP"] = 0
flag["add-position"]["count"] = 0
return flag
#------------バックテストの部分の関数--------------
# 各トレードのパフォーマンスを記録する関数
def records(flag,data,close_price,close_type=None):
# 取引手数料等の計算
entry_price = int(round(flag["position"]["price"] * flag["position"]["lot"]))
exit_price = int(round(close_price * flag["position"]["lot"]))
trade_cost = round( exit_price * slippage )
log = "スリッページ・手数料として " + str(trade_cost) + "円を考慮します\n"
flag["records"]["log"].append(log)
flag["records"]["slippage"].append(trade_cost)
# 手仕舞った日時と保有期間を記録
flag["records"]["date"].append(data["close_time_dt"])
flag["records"]["holding-periods"].append( flag["position"]["count"] )
# 損切りにかかった回数をカウント
if close_type == "STOP":
flag["records"]["stop-count"].append(1)
else:
flag["records"]["stop-count"].append(0)
# 値幅の計算
buy_profit = exit_price - entry_price - trade_cost
sell_profit = entry_price - exit_price - trade_cost
# 利益が出てるかの計算
if flag["position"]["side"] == "BUY":
flag["records"]["side"].append( "BUY" )
flag["records"]["profit"].append( buy_profit )
flag["records"]["return"].append( round( buy_profit / entry_price * 100, 4 ))
flag["records"]["funds"] = flag["records"]["funds"] + buy_profit
if buy_profit > 0:
log = str(buy_profit) + "円の利益です\n\n"
flag["records"]["log"].append(log)
else:
log = str(buy_profit) + "円の損失です\n\n"
flag["records"]["log"].append(log)
if flag["position"]["side"] == "SELL":
flag["records"]["side"].append( "SELL" )
flag["records"]["profit"].append( sell_profit )
flag["records"]["return"].append( round( sell_profit / entry_price * 100, 4 ))
flag["records"]["funds"] = flag["records"]["funds"] + sell_profit
if sell_profit > 0:
log = str(sell_profit) + "円の利益です\n\n"
flag["records"]["log"].append(log)
else:
log = str(sell_profit) + "円の損失です\n\n"
flag["records"]["log"].append(log)
return flag
# バックテストの集計用の関数
def backtest(flag):
# 成績を記録したpandas DataFrameを作成
records = pd.DataFrame({
"Date" : pd.to_datetime(flag["records"]["date"]),
"Profit" : flag["records"]["profit"],
"Side" : flag["records"]["side"],
"Rate" : flag["records"]["return"],
"Stop" : flag["records"]["stop-count"],
"Periods" : flag["records"]["holding-periods"],
"Slippage" : flag["records"]["slippage"]
})
# 連敗回数をカウントする
consecutive_defeats = []
defeats = 0
for p in flag["records"]["profit"]:
if p < 0:
defeats += 1
else:
consecutive_defeats.append( defeats )
defeats = 0
# テスト日数を集計
time_period = datetime.fromtimestamp(last_data[-1]["close_time"]) - datetime.fromtimestamp(last_data[0]["close_time"])
time_period = int(time_period.days)
# 総損益の列を追加する
records["Gross"] = records.Profit.cumsum()
# 資産推移の列を追加する
records["Funds"] = records.Gross + start_funds
# 最大ドローダウンの列を追加する
records["Drawdown"] = records.Funds.cummax().subtract(records.Funds)
records["DrawdownRate"] = round(records.Drawdown / records.Funds.cummax() * 100,1)
# 買いエントリーと売りエントリーだけをそれぞれ抽出する
buy_records = records[records.Side.isin(["BUY"])]
sell_records = records[records.Side.isin(["SELL"])]
# 月別のデータを集計する
records["月別集計"] = pd.to_datetime( records.Date.apply(lambda x: x.strftime('%Y/%m')))
grouped = records.groupby("月別集計")
month_records = pd.DataFrame({
"Number" : grouped.Profit.count(),
"Gross" : grouped.Profit.sum(),
"Funds" : grouped.Funds.last(),
"Rate" : round(grouped.Rate.mean(),2),
"Drawdown" : grouped.Drawdown.max(),
"Periods" : grouped.Periods.mean()
})
print("バックテストの結果")
print("-----------------------------------")
print("買いエントリの成績")
print("-----------------------------------")
print("トレード回数 : {}回".format( len(buy_records) ))
print("勝率 : {}%".format(round(len(buy_records[buy_records.Profit>0]) / len(buy_records) * 100,1)))
print("平均リターン : {}%".format(round(buy_records.Rate.mean(),2)))
print("総損益 : {}円".format( buy_records.Profit.sum() ))
print("平均保有期間 : {}足分".format( round(buy_records.Periods.mean(),1) ))
print("損切りの回数 : {}回".format( buy_records.Stop.sum() ))
print("-----------------------------------")
print("売りエントリの成績")
print("-----------------------------------")
print("トレード回数 : {}回".format( len(sell_records) ))
print("勝率 : {}%".format(round(len(sell_records[sell_records.Profit>0]) / len(sell_records) * 100,1)))
print("平均リターン : {}%".format(round(sell_records.Rate.mean(),2)))
print("総損益 : {}円".format( sell_records.Profit.sum() ))
print("平均保有期間 : {}足分".format( round(sell_records.Periods.mean(),1) ))
print("損切りの回数 : {}回".format( sell_records.Stop.sum() ))
print("-----------------------------------")
print("総合の成績")
print("-----------------------------------")
print("全トレード数 : {}回".format(len(records) ))
print("勝率 : {}%".format(round(len(records[records.Profit>0]) / len(records) * 100,1)))
print("平均リターン : {}%".format(round(records.Rate.mean(),2)))
print("標準偏差 : {}%".format(round(records.Rate.std(),2)))
print("平均利益率 : {}%".format(round(records[records.Profit>0].Rate.mean(),2) ))
print("平均損失率 : {}%".format(round(records[records.Profit<0].Rate.mean(),2) ))
print("平均保有期間 : {}足分".format( round(records.Periods.mean(),1) ))
print("損切りの回数 : {}回".format( records.Stop.sum() ))
print("")
print("最大の勝ちトレード : {}円".format(records.Profit.max()))
print("最大の負けトレード : {}円".format(records.Profit.min()))
print("最大連敗回数 : {}回".format( max(consecutive_defeats) ))
print("最大ドローダウン : {0}円 / {1}%".format(-1 * records.Drawdown.max(), -1 * records.DrawdownRate.loc[records.Drawdown.idxmax()] ))
print("利益合計 : {}円".format( records[records.Profit>0].Profit.sum() ))
print("損失合計 : {}円".format( records[records.Profit<0].Profit.sum() ))
print("最終損益 : {}円".format( records.Profit.sum() ))
print("")
print("初期資金 : {}円".format( start_funds ))
print("最終資金 : {}円".format( records.Funds.iloc[-1] ))
print("運用成績 : {}%".format( round(records.Funds.iloc[-1] / start_funds * 100),2 ))
print("手数料合計 : {}円".format( -1 * records.Slippage.sum() ))
print("-----------------------------------")
print("各成績指標")
print("-----------------------------------")
print("CAGR(年間成長率) : {}%".format( round((records.Funds.iloc[-1] / start_funds)**( 365 / time_period ) * 100 - 100,2) ))
print("MARレシオ : {}".format(round( (records.Funds.iloc[-1] / start_funds -1)*100 / records.DrawdownRate.max(),2 )))
print("シャープレシオ : {}".format( round(records.Rate.mean()/records.Rate.std(),2) ))
print("プロフィットファクター : {}".format( round(records[records.Profit>0].Profit.sum()/abs(records[records.Profit<0].Profit.sum()),2) ))
print("損益レシオ : {}".format(round( records[records.Profit>0].Rate.mean()/abs(records[records.Profit<0].Rate.mean()) ,2)))
print("-----------------------------------")
print("月別の成績")
for index , row in month_records.iterrows():
print("-----------------------------------")
print( "{0}年{1}月の成績".format( index.year, index.month ) )
print("-----------------------------------")
print("トレード数 : {}回".format( row.Number.astype(int) ))
print("月間損益 : {}円".format( row.Gross.astype(int) ))
print("平均リターン : {}%".format( row.Rate ))
print("継続ドローダウン : {}円".format( -1 * row.Drawdown.astype(int) ))
print("月末資金 : {}円".format( row.Funds.astype(int) ))
# 際立った損益を表示
n = 10
print("------------------------------------------")
print("+{}%を超えるトレードの回数 : {}回".format(n,len(records[records.Rate>n]) ))
print("------------------------------------------")
for index,row in records[records.Rate>n].iterrows():
print( "{0} | {1}% | {2}".format(row.Date,round(row.Rate,2),row.Side ))
print("------------------------------------------")
print("-{}%を下回るトレードの回数 : {}回".format(n,len(records[records.Rate< n*-1]) ))
print("------------------------------------------")
for index,row in records[records.Rate < n*-1].iterrows():
print( "{0} | {1}% | {2}".format(row.Date,round(row.Rate,2),row.Side ))
# ログファイルの出力
file = open("./{0}-log.txt".format(datetime.now().strftime("%Y-%m-%d-%H-%M")),'wt',encoding='utf-8')
file.writelines(flag["records"]["log"])
# 損益曲線をプロット
plt.subplot(1,2,1)
plt.plot( records.Date, records.Funds )
plt.xlabel("Date")
plt.ylabel("Balance")
plt.xticks(rotation=50) # X軸の目盛りを50度回転
# リターン分布の相対度数表を作る
plt.subplot(1,2,2)
plt.hist( records.Rate,50,rwidth=0.9)
plt.axvline( x=0,linestyle="dashed",label="Return = 0" )
plt.axvline( records.Rate.mean(), color="orange", label="AverageReturn" )
plt.legend() # 凡例を表示
plt.show()
#------------ここからメイン処理--------------
# 価格チャートを取得
price = get_price(chart_sec,after=1451606400)
flag = {
"position":{
"exist" : False,
"side" : "",
"price": 0,
"stop":0,
"stop-AF": stop_AF,
"stop-EP":0,
"ATR":0,
"lot":0,
"count":0
},
"add-position":{
"count":0,
"first-entry-price":0,
"last-entry-price":0,
"unit-range":0,
"unit-size":0,
"stop":0
},
"records":{
"date":[],
"profit":[],
"return":[],
"side":[],
"stop-count":[],
"funds" : start_funds,
"holding-periods":[],
"slippage":[],
"log":[]
}
}
last_data = []
need_term = max(buy_term,sell_term,volatility_term)
i = 0
while i < len(price):
# ドンチャンの判定に使う期間分の安値・高値データを準備する
if len(last_data) < need_term:
last_data.append(price[i])
flag = log_price(price[i],flag)
time.sleep(wait)
i += 1
continue
data = price[i]
flag = log_price(data,flag)
# ポジションがある場合
if flag["position"]["exist"]:
if stop_config != "OFF":
flag = stop_position( data,flag )
flag = close_position( data,last_data,flag )
flag = add_position( data,flag )
# ポジションがない場合
else:
flag = entry_signal( data,last_data,flag )
last_data.append( data )
i += 1
time.sleep(wait)
print("--------------------------")
print("テスト期間:")
print("開始時点 : " + str(price[0]["close_time_dt"]))
print("終了時点 : " + str(price[-1]["close_time_dt"]))
print(str(len(price)) + "件のローソク足データで検証")
print("--------------------------")
backtest(flag)