前回の記事では、以下のような破産確率の公式を紹介しました。また実際にpythonを使ってこの方程式を解いて、破産確率を計算する方法を解説しました。
前回学習した破産確率の公式
・勝率をP、損益レシオをkとするとき、
$$\begin{array}{l}
Px^{k+1} +( 1-P) -x=0\ \ \ の方程式の解で\ 、\\
\ 0< x< 1\ の範囲の\ x\ を\ x=R\ とする。
\end{array}$$
$${\Large 破産確率\ =\ R^{\frac{資金額}{1回あたりの損失} \ }}$$
上記の方程式の解Rは、トレードの期待値が0円を上回るとき、必ず0<R<1の範囲に1つ存在し、かつ勝率や損益レシオが高ければ高いほど小さい数字になることも学習しました。詳しくは、前回の2記事を確認してください。
FXトレードの破産確率を高校数学で理解しよう!(1)
FXトレードの破産確率を高校数学で理解しよう!(2)
さて今回はこの公式を前提として、最終的に実践のトレードで使える破産確率の公式を作り、実際にpythonでBOTの破産確率を計算してみます!
1回の損失額が定まらない場合
前回の最後でも説明しましたが、上記の公式のままでは残念ながらまだ実践のトレードでは使えません。なぜなら、実践では1回のトレードの損失額を一定額に固定できないからです。
例えば、第7回の「資金管理編」では、毎回、口座残高のX%だけリスクを取り、そのリスクの範囲内でポジションサイズを計算する方法を紹介しました。この方法の場合、毎回の賭け金(トレードでリスクに晒す金額)は、そのときの口座残高に応じて毎回変動します。
「毎回1万円を賭ける」と決まっているゲームであれば、上記の公式をそのまま使うことができます。ですが、トレードのように毎回の損失額を固定できないゲームでは、上記の公式を使って破産確率を計算することはできません。
1.「資金量」の意味
では、もう少し踏み込んで考えてみましょう。前々回の記事で紹介した一番簡単な基本公式を思い出してください。以下のような公式でしたね。
基本の公式
・勝ったら1円の利益、負けたら1円の損失、というトレードで、勝率と資金量の2つの値から破産確率を計算する公式
$${\Large 破産確率\ =\ \left( \ \frac{負ける確率}{勝つ確率} \ \right)^{資金の量}}$$
ここでいう「資金量」とは何でしょうか?
「勝ったら1円貰える」「負けたら1円失う」という前提のゲームですから、資金量とは、言い換えれば「何回まで負けることができるか?」という最大負け回数に置き換えて考えることができます。必ずしも単位は円でなくてもいいのです。
この回数のことをトレードの世界では「ユニット数」と表現することがあります。要するに、資金量から考えて「何回トレードできるのか?」という回数がユニット数です。
$${\Large 破産確率\ =\ \left( \ \frac{負ける確率}{勝つ確率} \ \right)^{ユニット数}}$$
また前回の記事で解説しましたが、破産確率の公式はすべてこの基本公式から派生しています。損益レシオが異なる場合や、1回の損失額が大きい場合も、すべて「1円ゲームに換算して考える」と言ったのを思い出してください。
つまり最初の公式も全く同じように資金量のところを「ユニット数」に置き換えることができます。
2.トレードできる最大回数がわかる場合の公式
・勝率をP、損益レシオをkとし、
・資金からトレードできる最大回数を「ユニット数」とするとき、
$$\begin{array}{l}
Px^{k+1} +( 1-P) -x=0\ \ \ の方程式の解で\ 、\\
\ 0< x< 1\ の範囲の\ x\ を\ x=R\ とする。
\end{array}$$
$${\Large 破産確率\ =\ R^{ユニット数}}$$
例えば、初期資金が100万円で、「毎回のトレードでは1万円のリスクと取る」と決めて、そこから逆算して損切り幅やポジションサイズを設計している方であれば、ユニット数は100とすれば、上記の公式で破産確率を計算できることになります。
(例)BOTの成績と破産確率
・勝率 31.5%
・損益レシオ 2.99
・初期資金 100万円
・1回のトレードリスク 5万円
・ユニット数 20回
破産確率 = 3.76%
※ 計算方法は、前回の記事 を参照
要するに「資金からトレードできる最大回数」さえわかれば、そこから上記の公式で破産確率を計算できるのです。
3.口座の一定率のリスクを取る場合
ここで私たちが知りたい問題は、「毎回のトレードで口座の3%のリスクを取った場合の最大トレード回数(ユニット数)はいくつか?」という数学の問題だということに気付くことができました。
ではこのユニット数はいくつでしょうか?
鋭い方はすぐにわかるかもしれませんが、この問題は「いくらを撤退のラインとするか?」を決めないと決まりません。なぜなら「口座のX%のリスクでトレードする」というルールだけだと、口座資金がどれだけ減っても永久にトレードを続けることができるからです。
(例)口座の50%のリスクでトレード
100万円 ⇒ 50万円 ⇒ 25万円 ⇒ 12.5万円 ⇒ 6.25万円 ⇒ 3.125万円 ⇒ 1.5625万円 ⇒ 7812円 ⇒ 3906円・・・
そこで、まず先に「n円以下を破産とみなす」という実質的な撤退ラインを決めなければなりません。今回は以下のような例題を考えましょう。
例題
以下の場合のユニット数はいくつか?
1)初期資金100万円
2)資金10万円以下になったら撤退(破産とする)
3)口座の3%を賭けてトレードする
この問題は、実は対数(log)という考え方を使うと簡単に解くことができます。対数がわかる方は読み飛ばして構いませんが、対数を忘れている方もいるかもしれないので、対数について解説します。
4.対数(log)って何だっけ?
対数をズバリ一言で説明すると、「掛け算を足し算に変換するための数学ツール」です。
私と同じように高校数学が苦手だった方でも、FXを始めてから「対数チャート」というのを見たことがあると思います。例えば、以下はビットコイン現物価格の対数チャートです。
わかりやすい例なので、BTC現物価格の2013年~2018年3月の価格チャートと対数チャートを見てみましょう!
▽ 価格チャート
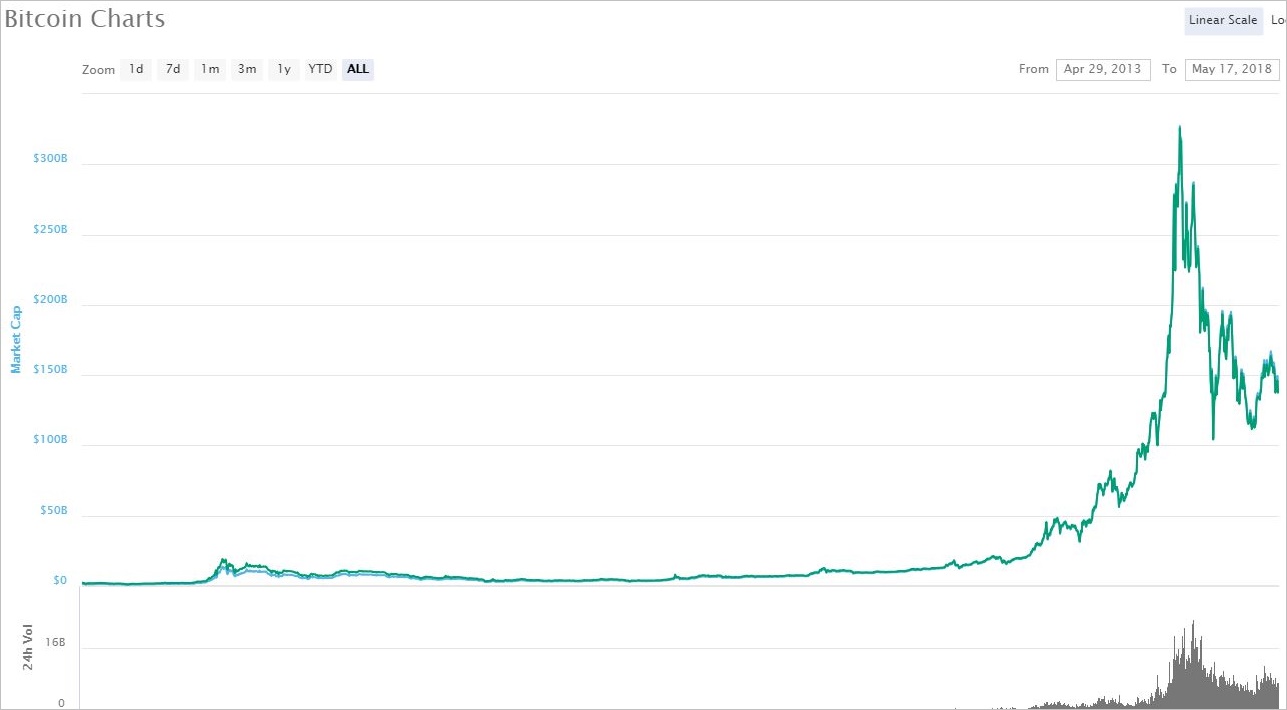
▽ 対数チャート
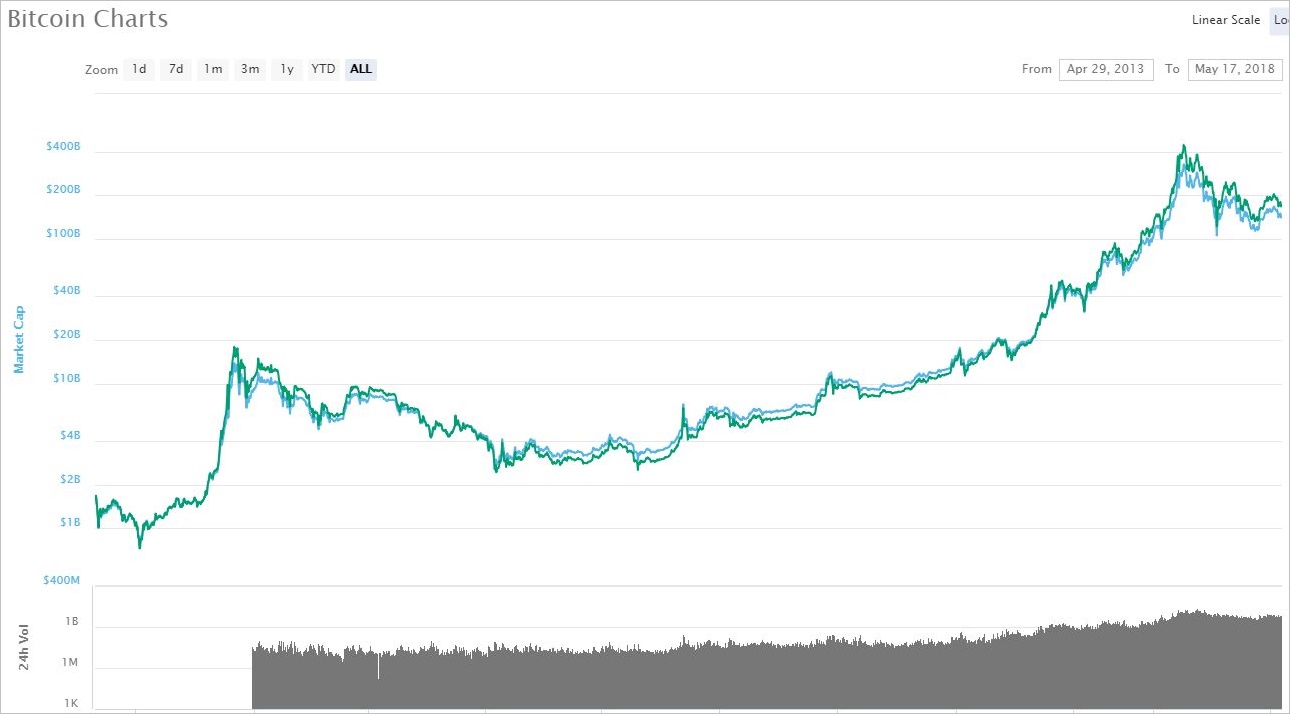
出典「CoinMarketCap」
上記の2つのチャートは全く同じ期間のものですが、全く別物のように見えます。その理由は以下です。
BTC価格が10万円から20万円になるのと100万円から200万円になるのとでは、同じ2倍でも価格チャート上の目盛りは大きく異なります。前者は10万円しか上がっていない一方、後者は100万円上がっています。そのため、価格チャートでは直近に極端に大きな値動きがあったように見えてしまいます。
しかし対数チャートでは、「2倍は同じ2倍」として扱います。つまり10万円が20万円になった場合と、100万円が200万円になった場合とを、y軸上で同じ目盛り幅(間隔)で表示します。そのため、「何倍になったか?」という視点で長い期間のチャートを見るときには、対数チャートを見たほうがわかりやすい、と言われます。
ここまでが一般的な説明です。
1)数式で理解してみよう!
では、これを数学的に理解してみましょう!
上記の説明をそのまま数式にすると以下のようになります。
▽ 価格チャートの場合
$$\begin{array}{l}
値動きA\ =\ 20万円-10万円\ =\ 10万円\\
値動きB\ =\ 200万円-\ 100万円\ =\ 100万円\\
\\
値動きB\ >\ 値動きA
\end{array}$$
▽ 対数チャートの場合
$$\begin{array}{l}
対数価格の差A\ =\ log20万-log10万\ =\ log( \ 20万\ /\ 10万) \ =\ log2\\
対数価格の差B\ =\ log200万-\ log100万\ =\ log( \ 200万/100万) \ =\ log2\\
\\
対数価格の差B\ =\ 対数価格の差A
\end{array}$$
後者の場合は、どちらも対数差分が log2 になるのがわかります。ちなみに、このことは高校で勉強する対数の「基本公式」から導き出せます。詳しくは以下のリンクを参考にしてください。
▽ 対数の基本公式
$$\begin{array}{l}
log_{a} M\ +\ log_{a} N\ =\ log_{a} MN\\
log_{a} M\ -\ log_{a} N\ =\ log_{a}\frac{M}{N} \
\end{array}$$
参考:「対数の基本的な性質と証明」
2)対数は掛け算を足し算に、割り算を引き算にする
上記の公式を見るとわかりますが、これは逆にいうと「対数を取れば掛け算を足し算に(割り算を引き算に)できる」ということだとわかります。例えば、「価格が2倍になった」という数式の対数を取ってみましょう。
$$\begin{array}{l}
100000\ \times \ 2\ =\ 200000\\
\\
両辺の対数を取ると\\
\\
log( 100000\ \times 2) \ =\ log200000\ \\
\\
左辺に公式を使うと\\
\\
log100000\ +\ log2\ =\ log200000=\ 12.2060726…
\end{array}$$
これが、「掛け算は対数を取ると足し算にできる」という意味です。なお、上記の式が本当にそうなるのか気になる方は、pythonで以下を実行してみてください。
▽ pythonで計算して確認してみよう!
import numpy as np print(np.log(2) + np.log(100000)) print(np.log(2 * 100000)) print(np.log(200000))
3)口座の一定率をリスクに晒す場合のトレード回数
本題に戻りましょう!
この考え方を利用すると「1回のトレードで口座の3%を失う」という状態を引き算(または足し算)で表すことができます。
以下のような具合です。
$$\begin{array}{l}
口座残高\ =\ 100万\ \times \ 0.97\ \times \ 0.97\ \times \ 0.97\ \times \ 0.97\ …..\\
口座残高の対数\ =\ log100万\ +\ log0.97\ +\ log0.97\ +\ log0.97…..
\end{array}$$
これが成り立つということが、あまりピンと来ない方は、ぜひpythonでlog0.97を計算してみてください。log0.97 = -0.0304592…となり、マイナスの数字であることがわかります。
ということは、口座の残高の対数を log0.97 で割れば、定率3%で何回トレードできるか数えることができそうですね! 実際にやってみましょう!
定率の場合の公式
$${\large ユニット数U\ =\frac{log資金\ -\ log撤退ライン}{| log( 1-リスク率)| }}$$
$${\large 破産確率\ =\ R^{U}}$$
できました!
実際の数字を入れてみた方がイメージが湧きやすいので、本当にこれでユニット数が計算できるのかどうか、やってみましょう!
4)定率のユニット数を計算するコード
import numpy as np
funds = 1000000 # 初期資金
risk_rate = 0.1 # 1回のトレードで取るリスク率
bankrupt_line = 200000 # 撤退ライン(破産)
unit = (np.log(funds) - np.log(bankrupt_line)) / abs(np.log( 1-risk_rate ))
unit = int(np.floor(unit)) # 切り捨て
print("最大{}回までトレードできます".format(unit))
先ほども説明したように、口座の一定率のリスクを取る場合は撤退ラインを決めておかないと、永遠にトレードができてしまいます。必ず撤退ラインを入力するようにしてください。
では、試しに以下のようなテストしやすい例を考えてみましょう。
(テスト条件)
・初期資金 100万円
・撤退ライン 20万円
・口座のリスク 10%
100万円から始めて、毎回のトレードで口座の10%までリスクを取った場合です。これは実際に電卓で計算してみると以下のようになります。
100万円 ⇒ 90万円 ⇒ 81万円 ⇒ 72.9万円 ⇒ 65.6万円 ⇒ 59万円 ⇒ 53万円 ⇒ 47.8万円 ⇒ 43万円 ⇒ 38.7万 ⇒ 34.8万円 ⇒ 31.3万円 ⇒ 28.2万円 ⇒ 25.4万円 ⇒ 22.8万円 ⇒ 20.5万円 ⇒ 18.5万円
つまり撤退ラインに達する(破産する)までに最大15回トレードできることがわかります。ユニット数は15です。
では上記のコードを実行してみましょう。
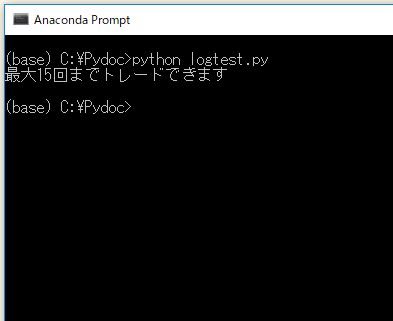
ちゃんと最大トレード回数を計算できています。
これで「口座のX%のリスクを取ってトレードする場合」でもユニット数を計算して、破産確率を算出できるようになりました。
4.破産確率を計算するpythonコード
では、前回の記事で作成した「特性方程式を解いて破産確率を計算するpythonコード」に、今回のユニット数を計算する箇所を付け足しましょう!
これで破産確率の計算コードは完成です!
import numpy as np
# 設定値
winning_percentage = 0.375 # 勝率
payoff_ratio = 2.09 # 損益レシオ
funds = 1000000 # 初期資金
risk_rate = 0.05 # 1回のトレードで取るリスク率
bankrupt_line = 200000 # 撤退ライン(破産)
# 特性方程式の関数
def equation(x):
k = payoff_ratio
p = winning_percentage
return p * x**(k+1) + (1-p) - x
# 特定方程式の解を探す
def solve_equation():
R = 0
while equation(R) > 0:
R += 1e-4
if R>=1:
print("期待値が0を下回っています")
R=1
print("特性方程式の解は{}です".format(R))
return R
# 破産確率を計算する公式
def calculate_ruin_rate( R ):
unit = (np.log(funds) - np.log(bankrupt_line)) / abs(np.log( 1-risk_rate ))
unit = int(np.floor(unit))
return R ** unit
# メイン処理
R = solve_equation()
ruin_rate = calculate_ruin_rate(R)
print("破産確率は{}%です".format( round(ruin_rate * 100,2) ))
5.練習~破産確率からリスク率を考えよう
では試しに以下のような、チャネルブレイクアウトBOTを考えてみましょう。
BOTの成績と資金条件
・勝率 37.5%
・平均利益率 8.21%
・平均損失率 3.92%
・損益レシオ 2.09
・初期資金 100万円
・撤退ライン 20万円
一応、期待値はプラスなので運用すること自体は可能なBOTです。では1トレードで取る口座のリスクは何%で運用するのが適切でしょうか?
試しに口座のリスク率を1%から順番に計算してみると以下のようになります。
| 口座のリスク率 | 破産確率 |
|---|---|
| 1% | 0.0% |
| 2% | 0.0% |
| 3% | 0.04% |
| 4% | 0.31% |
| 5% | 1.01% |
| 6% | 2.11% |
| 7% | 3.82% |
| 8% | 5.96% |
| 9% | 8.03% |
| 10% | 10.8% |
上記のBOTはそれほど成績が優秀なわけではありませんが、それでも教科書通り、口座のリスクを1~3%の範囲におさえて運用していれば、破産リスクはほとんどないことがわかります。
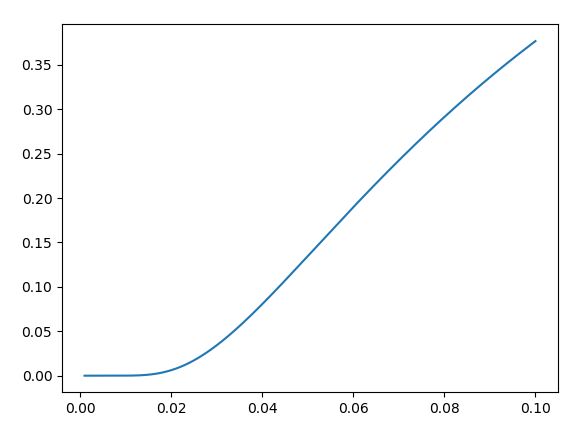
逆に口座リスクが5%を超えたあたりから、急激に破産リスクが上がっています。実際に上記の破産確率の公式で、0.1%刻みで破産確率を計算した結果をプロットすると以下のようになりました。
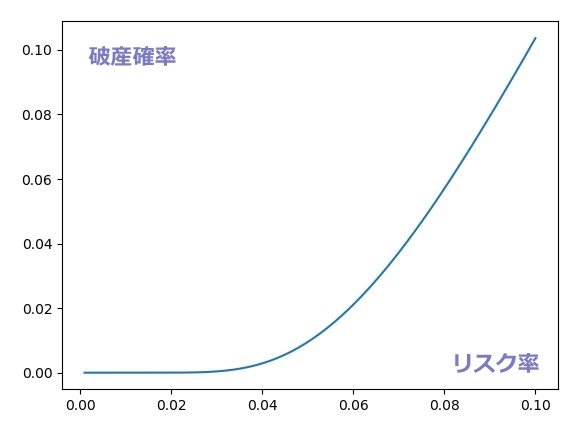
以前にこちらの記事でも解説したように、口座の5%以上のリスクを取ると、うまくいけば高い運用パフォーマンスを手にすることができます。しかし逆に失敗したときの破産確率も、急速に「現実におこりうる数字」に近づくのがわかります。
どの程度までリスクを許容するかは、運用資金の大きさにもよりますが、教科書的には1~2%未満におさえるのが良いとされています。
6.許容ドローダウンから考える
「破産確率」という名前こそ付いていますが、実際には上記の計算式は「許容ドローダウン」を考えるのに活用した方が実用的です。
例えば、さきほどは撤退ライン(破産ライン)を20万円としましたが、数百万円以上の資金を運用している人からすると、実際には50%すら失いたくない人が大半でしょう。つまり撤退ライン(破産ライン)を50万円で計算する必要がありますが、この場合の計算結果はもっとシビアになります。
許容ドローダウンが50%の場合
・勝率 37.5%
・平均利益率 8.21%
・平均損失率 3.92%
・損益レシオ 2.09
・初期資金 100万円
・破産ライン 50万円
| 口座のリスク率 | 破産確率 |
|---|---|
| 1% | 0.0% |
| 2% | 0.64% |
| 3% | 3.82% |
| 4% | 9.31% |
| 5% | 14.53% |
| 6% | 19.55% |
| 7% | 26.3% |
| 8% | 30.51% |
| 9% | 35.39% |
| 10% | 41.05% |
この成績のBOTで1回のトレードで口座の5%のリスクを取った場合、約1/10の確率で50%のドローダウンに見舞われることになります。口座の10%のリスクを取ると、なんと40%の確率で半分の資金を失うことになるのです。これを許容できる人は少ないでしょう。
一方、こちらの場合でも口座リスク2%までであれば、50%のドローダウンがおこる確率はほとんど無いことがわかります。多くのトレードの教科書で「2%ルール」が推奨されるのは、この辺りの特徴にも理由があるのかもしれません。
なお、ここまでの数式を追っていただいた方ならわかると思いますが、上記の破産確率の公式は、初期資金200万円、撤退ライン100万円で試しても、初期資金2000万円、撤退ライン1000万円で試しても全く同じです。要するに、ドローダウン率50%の確率表です。
次回
次回は、前章までで作成した「すでに損益レシオと勝率がわかっているBOT」について、許容ドローダウン率と口座のリスク率をそれぞれ縦軸と横軸に取った破産確率表をCSVで出力する方法を紹介して、最後の記事とする予定です。個人的にはそれが最も実用的な破産確率表の使い方ではないかと思います。