はじめにお断りしておくと、私自身が私大文系の出身で数学はもともと苦手です。
社会人になってから興味をもって少しだけ勉強するようになりましたが、それでも高校数学の範囲も復習しないと自信がありません。この記事は、同じレベルの方でも何となく破産確率を理解できることを目指します。
バルサラの破産確率表
よく「FX 破産確率」などで検索すると、バルサラ破産確率表なるものがズラっと出てきます。列に「損益レシオ」、行に「勝率」が記載された表で、見たことがある方もいるかもしれません。
▽ Google検索の「バルサラ破産確率表」
しかしその多くは前提条件や計算根拠が不明なまま転載されている表で、あまり役に立ちません。破産確率は「資金の量」によって決まる関数なので、資金の量を聞かれてないのに破産確率だけわかる、ということは基本的にありえません。
おそらく出回っているバルサラ破産確率表は、「口座のn%を毎回トレードで賭ける」「口座がk%まで減ったら破産とみなす」という前提条件があるはずで、それこそが知りたい数字なのですが、そこまで記載されていることも少ないです。
前提
私は以下のページを参考にさせて貰い、熟読してやっと破産確率の正しい計算方法を何となく理解することができました。数学が得意な方は、おそらく直接以下のページを読んだ方が理解が早いと思います。
「チンプンカンプンだ….」という方は、私と同じなので安心してください。私もわざわざ「漸化式って何….?」「等比数列の和の公式って何だっけ?」というレベルから復習してやっとわかりました(笑)
この記事では、最低限、高校数学Bの確率と数列(等比数列の公式など)が登場します。ただそれがわからない方でも、破産確率の式が何を意味しているのか、何となくわかるように説明したいと思います。
勝率についての公式
まず最初にもっとも簡単な公式から確認していきましょう。
以下の前提条件を満たすとき、この公式が成り立ちます。
前提条件
1)勝ったら1円の利益、負けたら1円の損失というトレード
2)市場の資金は無限と仮定する
3)勝率は50%を超えていると仮定する
公式
$${\Large 破産確率\ =\ \left( \ \frac{負ける確率}{勝つ確率} \ \right)^{資金の量}}$$
この条件では、勝率が50%以下のときに期待値が0円を下回ります。そのため、半永久的にトレードを繰り返すといつか必ず破産します。この「期待値が0円を下回る場合、ずっとトレードを繰り返すといつか必ず破産する」という考え方は、今後も使うので覚えておいてください。
この公式からわかること
この時点でわかることは、「言われなくても知ってるよ!」という当たり前のことばかりですが、一応、数式で確認しておきましょう。
勝率が50%を超えるという前提ですから、()の中の数字は必ず1未満になります。そして勝率が大きければ大きいほど、中身は小さな数字になります。つまり勝率が高いほど、破産確率は小さくなります。
また「勝つと1円儲かる」「負けると1円損する」というのが前提ルールですから、資金が多ければ多いほど破産確率は低くなるはずですし、実際、そうなっています。()の中の数字は必ず1未満の数字ですから、乗数は大きければ大きいほど、破産確率は小さくなります。
例)
$$0.8\ >\ 0.8^{2} \ >\ 0.8^{3} \ >\ 0.8^{4} \ ….$$
この最初の公式だけでも、「資金量を聞かれてないのに破産確率がわかるのはおかしい」と判断できますね。この公式は、今後のさらに実践的な公式の基礎となる部分なので、ぜひ押さえておいてください。
1)高校数学の「確率」から考える
では、なぜ上記のような式になるのか確認しておきましょう。まずはスタートとして、高校数学の「確率」から考えます。資金がn円のときに破産する確率をQ(n)とします。
例えば、現在の所持金を100円だと仮定しましょう。今が何回目のトレードかはわかりません。わかりませんが、とにかく何回目かのトレードの時点で所持金が100円になりました。所持金100円なので、もちろんまだ破産していません。
所持金100円の時点から将来的に破産する確率は、Q(100)です。ここまでは問題ないと思います。
では、さらに所持金100円の次に取りうる状態を考えてみましょう。「勝ったら1円儲かる」「負けたら1円失う」というトレードですから、次の所持金は、勝って101円になるか、負けて99円になるか、の2通りしかありません。
つまり「所持金100円で破産する確率」というのは、以下の2つの確率の合計で表すことができます。(Pは勝率)
1)所持金100円で将来的に破産する確率 Q(100)
2)次に所持金101円になって将来的に破産する確率 Q(101) × P
3)次に所持金99円になって将来的に破産する確率 Q(99) × (1-P)
(数式)
$${\small Q( 100) \ =\ Q( 101) \times P\ +\ Q( 99) \times ( 1-P) \ }$$
ここまでは大丈夫でしょうか?
2)漸化式にする
上記の式は、どの資金額の時点でも同じですから、以下のように一般化することができます。
$$Q( n) \ =\ Q( n+1) \times P\ +\ Q( n-1) \times ( 1-P) \ $$
これは私と違って高校時代にちゃんと数学を勉強していた方なら、見覚えがあるかもしれません(笑)。「漸化式」というやつですね。もっと具体的にいうと、3項間漸化式(特性方程式)というジャンルの問題です。
さすがにここで漸化式の解き方を0から解説すると終わらなくなるので、もし漸化式がわからない方は以下のYouTube講義動画を見てください。めちゃくちゃわかりやすいです。私の高校時代もこうやって教えて欲しかった…。
では同じやり方で解いてみましょう。
3)特性方程式を解く
$${\small Q( n) \ =\ P\cdotp Q( n+1) \ +\ ( 1-P) \cdotp Q( n-1)}$$
まずは高校数学の教科書と同じ感じになるように、Q(n-1) を an に置き換えましょう。
$$a_{n+1} \ =\ P\cdotp a_{n+2} \ +\ ( 1-P) \cdotp a_{n}$$
するとこれは高校で習う三項間漸化式の問題なので、以下のような特性方程式を考えます。この特性方程式の解を使うと、上記の式を綺麗に変形することができるからです。
(特性方程式)
$$x\ =\ P\cdotp x^{2} \ +\ ( 1-P)$$
この方程式を因数分解すると以下のようになります。
$${\small P( x-1)\left( x-\frac{1-P}{P}\right) \ =\ 0}$$
$$よって解は、\ x\ =\ \ 1,\ \frac{1-P}{P}$$
このことから、特性方程式の性質(二次方程式の「解と係数の関係」)を使って、最初の式は以下のように変形できます。
$$a_{n+2} \ -\ a_{n+1} \ =\ \frac{1-P\ }{P}( a_{n+1} \ -\ a_{n})$$
これは、公比が (1-P)/P の階差数列です。
階差数列というのは、各項目の間隔が等比数列や等差数列になっている順列のことです。つまり、破産確率の関数Q(n)は、資金が1円ずつ増えるたびに、どんどん破産の可能性が低くなるものの、その減り幅は ×(1-p)/P ずつ狭くなる関数だということがわかります。
さて、上記は階差数列なので、以下の公式を使うと a(n) の一般項を求めることができます。(階差数列の公式)
$$\begin{array}{l}
a_{n+1} -a_{n} \ の部分を\ b_{n} とおくと、\\
\\
b_{n+1} =\left(\frac{1-P}{P}\right) b_{n} \ \ となるので、\ b_{n} は公比数列です。\\
\\
公比数列の公式により、b_{n} \ の一般項は、\\
\\
b_{n} =b_{1} \ \cdotp \left(\frac{1-P}{P}\right)^{n-1} となります。\\
\\
\\
そのため、n\ \geq 2\ のときの\ a_{n} の一般項は、\\
\\
a_{n} \ =\ a_{1} +{\displaystyle \sum ^{n-1}_{k=1} b_{k}}\\
\\
=a_{1} +{\displaystyle \sum ^{n-1}_{k=1} \ ( a_{2} \ -\ a_{1}) \cdotp \ \left(\frac{1-P}{P}\right)^{k-1} \ }\\
\\
=a_{1} +( a_{2} -a_{1}){\displaystyle \sum\limits ^{n-1}_{k=1}\left(\frac{1-P}{P}\right)^{k-1}}\\
\\
となります\\
\
\end{array}$$
では、これを最初の破産確率の Q(n) に戻してみましょう。
すると以下のようになりますね。
$$Q( n) =Q( 0) +( Q( 1) -Q( 0)) \cdotp {\displaystyle \sum ^{n}_{k=1}} \ \left(\frac{1-P}{P}\right)^{k-1}$$
また資金が0円のときの破産確率 Q(0) は当然、100%(=1)です。そのため、Q(0) には1を代入していきます。ついでに見やすいように、(1-P)/P はいったん、rと置き換えましょう。
$$Q( n) =1+( Q( 1) -1) \cdotp {\displaystyle \sum ^{n}_{k=1}} \ r^{k-1}$$
「数列の和の公式」を使えば、シグマも外すことができますね。
これも外しておきましょう。
$$Q( n) =1+( Q( 1) -1) \cdotp \left(\frac{r^{n} -1\ }{r-1}\right)$$
これでいったん完成です。
ですが、まだ最初のシンプルな公式からは程遠いですね。破産確率 Q(1)の正体がわかれば、一気に公式に辿り着けるのですが、この時点ではまだQ(1)が何かはわかりません。
・Q(1) ⇒ 資金が1円のときに将来破産する確率
例えば、資金が1円で勝率が80%の場合、破産確率 Q(1) は、パッと考えると 20%のような気もしますが、そう簡単ではありません。もし次のトレードで勝って破産を免れたとしても、その後に2連敗すれば破産します。もし次とその次のトレードに勝っても、その後に3連敗すれば破産します。
つまり勝率80%の中に、まだ将来破産する確率 Q(2) が含まれていて、資金2円の時点での勝率には 将来破産する確率Q(3)が含まれているので、結局、堂々巡りになるわけです。
実は、この資金が1円のときの破産確率 Q(1) は、負けのオッズ比 、つまり (1-P)/P にピッタリ一致するのですが、そのことは違うアプローチから証明することになります。
4)相手の資金量から破産確率を考える
現実的には、FXのトレードで世界中の資金を奪いつくすことはできません。ですが、数学はただの想像の世界なので、自由な仮定を置くことができます。例えば、相対取引でトレードの相手方の資金がX円であるような場合を考えましょう
「勝ったら1円貰える」「負けたら1円失う」というトレード勝負は、前提として勝率が50%以上という偏りがある以上、半永久的に繰り返せば必ずいつか終わります。つまり、相手の資金を奪いつくしたら終わるわけです。
この相手の資金を奪いつくした時点での自分の資金量を、仮に m円 とします。すると、m円の時点での破産確率は、Q(m)=0 となります。もう破産する可能性が無くなったからです。
$${\large Q( m) \ \ =\ 0\ }$$
これを先ほどの公式に当てはめると、以下のような方程式を作ることができます。
(方程式)
$$Q( m) =1+( Q( 1) -1) \cdotp \left(\frac{r^{m} -1\ }{r-1}\right) \ =0$$
これを頑張って展開すると、さっき未知数だった Q(1) を 相手の資金量 m円 を使って式に表すことができます。具体的にやってみるとわかりますが、以下のような式にできます。
※ 展開した後、分母と分子の両方に-1を掛けています。
$$Q( 1) \ =\ \frac{r-r^{m}}{1-r^{m}} \ $$
さて、現実の世界に戻りましょう。
実際のトレードの世界では、私のような普通の一般人が取引所や市場の資金を奪いつくすことはありえません。つまり、「相手の資金を奪いつくした時点での資金 m円」というのは、現実には辿り着けるはずのない、非常に大きい数字だと考えることができます。
さらに、r というのは何だったかを思い出してみましょう。
rで置き換えたのは、(1-P)/P で、これは「負ける確率 ÷ 勝つ確率」でしたね。これは勝率が50%を超えるとき、必ず1より小さい数になります。
以下の式を見てみると、rのm乗というのは、この1よりも小さい数をとてつもなく大きい指数で乗じたものです。

そのため、こちらの自己資金よりも相手の資金(市場の資金)がとてつもなく大きいときには、この「rのm乗」は無視していいほど小さな数字になります。
結果、さきほどわからないといった 資金1円のときの破産確率 Q(1) は、「市場の資金がとてつもなく大きい」という前提のもとでは、以下のようになるのです。
$$Q( 1) =\frac{r-r^{m}}{1-r^{m}} =r=\ \left(\frac{1-P}{P}\right)$$
例えば、勝率80%、負率20%のトレードを資金1円でスタートしたら、1/4の確率(25%)で破産するということですね。
では、ここで Q(1)=r とわかったので、さきほど「いったん完成」と言っていた式に代入してみましょう。
$$\begin{array}{l}
Q( n) =1+( Q( 1) -1) \cdotp \left(\frac{r^{n} -1\ }{r-1}\right)\\
\\
=\ 1+( r-1) \cdotp \left(\frac{r^{n} -1}{r-1}\right)\\
=1+\left( r^{n} -1\right)\\
=r^{n}\\
\\
=\left(\frac{1-P}{P}\right)^{n}
\end{array}$$
驚くほど気持ちよく消えてシンプルな式になります。
これで最初の公式に辿り着くことができました!
お疲れ様でした!
$${\large 破産する確率\ Q( n) \ =\ \left(\frac{1-P}{P}\right)^{n}}$$
次回
この公式だけでは、実際のトレードではあまり役に立ちません。実際のトレードでは、勝率が50%以上とは限りませんし、平均利益と平均損失の割合も違いますし、さらに毎回のエントリー価格やロット数(賭け金)も異なります。
次回の記事は、この続きで「平均利益と平均損失が異なる場合」について解説します。さらに「口座の一定率をリスクに晒す場合(毎回の賭け金が異なる場合)」について解説し、最終的にはpythonを使って、口座のリスク割合ごとの破産確率をシミュレーションできるようにする予定です。
すべての指標やツールは、何らかの具体的な意思決定に役立ってはじめて意味があります。「へぇ、私のBOTの破産確率は〇%なんだ」という感想で終わったら実用性はありません。実際に口座のリスク率を決定するときの判断材料として役立つようなpythonコードを作っていきましょう。
次回の記事:
FXの破産確率を高校数学で理解しよう!(2)
追記
その後さらに調べたところ、巷に出回っているバルサラ破産確率表は、ナウザー氏の著書から転載されていたようです。原著を確認したところ、前提条件は「所持金1円の状態で1円を賭けてトレードした場合」と「所持金2円の状態で1円を賭けてトレードした場合」の破産確率でした。
▽ 原著の破産確率表
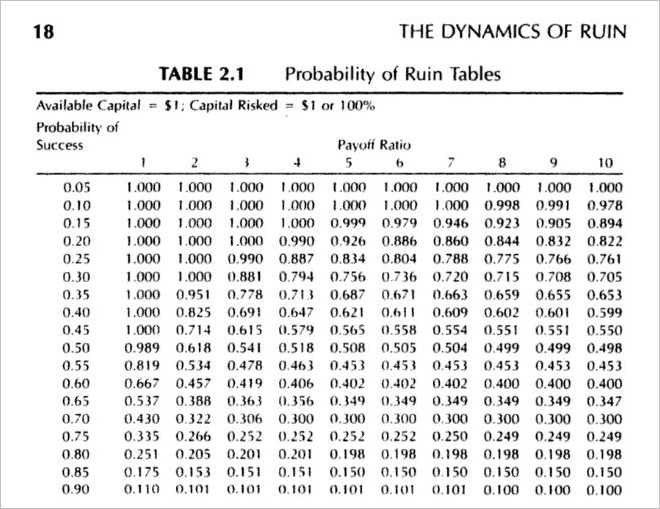
出典「Money Management Strategies for Futures Traders」
これは「1回のトレードですべての資金を失うようなリスクを取った場合」の破産確率なので、実際のトレードでは少し考えにくい資金条件ですが、これを正しく転載していれば、数字自体は一致することが確認できました。