前回の記事の続きです。
今回はより実践的なFXトレードでの破産確率の公式を紹介し、さらにpythonを使って実際に破産確率を計算します。 なお今回の内容は、前回の「基本公式」が前提となっているため、なぜ以下の式が導き出せるのかわからない方は、先に前回の記事を読むことを推奨します。
基本の公式
・勝ったら1円の利益、負けたら1円の損失、というトレードで、勝率と資金量の2つの値から破産確率を計算する公式
$${\Large 破産確率\ =\ \left( \ \frac{負ける確率}{勝つ確率} \ \right)^{資金の量}}$$
前回の記事:
・FXの破産確率を高校数学で理解しよう!(1)
では始めましょう!
1回の賭け金を増やした場合の公式
前回の記事では、「勝ったら1円の利益」「負けたら1円の損失」というトレードを無限に繰り返した場合に、勝率(P)と資金(N)がどのように破産確率に影響を与えるか、を確認しました。
しかし実際のトレードでは、当然、賭け金は1円ではありません。そこで、まずは以下のような条件での破産確率の公式を考えてみましょう。
前提条件
1)勝ったら1000円の利益、負けたら1000円の損失というトレード
2)市場の資金は無限と仮定する
3)勝率は50%を超えていると仮定する
実はこの場合の破産確率の公式は「めちゃめちゃ簡単」です。
以下のように変形するだけでいいのです。
$${\Large 破産確率\ =\ \left(\frac{負ける確率}{勝つ確率} \ \right)^{\frac{資金の額\ }{1000円\ }}}$$
要するに、右上の指数の「資金量」を「1トレードあたりの損失額」で割ればOKです。なぜそうなるかは後述します。
公式からわかること
上記の公式から、同じ勝率でも1トレードあたりの損失額(=賭け金)が大きければ大きいほど、破産確率は大きくなることがわかります。
勝率が50%を超えるという前提条件があるため、()の中身は必ず1未満の数字になります。そのため、右上の指数は大きければ大きいほど、破産確率は小さくなります。例えば、資金量が多ければ多いほど、同じ勝率でも破産確率は低くなります。
逆に右上の指数が小さくなると、破産確率は大きくなってしまいます。そのため、1回のトレードの賭け金の額を増やすと、破産確率は大きくなります。
賭け金の定義
ちなみにトレードにおける「賭け金」の定義をここで整理しておいてください。賭け金はエントリー価格やサイズのことではありません。最終的に1回のトレードで失う証拠金(例えば、損切り幅)のことです。「ポジションを持つために投入した金額」ではないので注意してください。
上記の式になる理由
初期資金10万円で「勝ったら1000円の利益」「負けたら1000円の損失」のトレードをすることは、初期資金100円で「勝ったら1円の利益」「負けたら1円の損失」のトレードの破産確率を計算するのと全く同じです。
つまり賭け金の額が大きい場合は、その分だけ口座資金を小さくして考えれば、前回に学習したのと同じ「勝ったら+1円」「負けたら-1円」のゲームに変換することができます。この考え方は、これから先の破産確率の公式でも全て同じです。
どんな条件でも、基本的には「資金額」の方をうまく調整して、すべて「1円ゲーム」に換算して考えます。例えば、以下のような条件を考えてみてください。
・初期資金100万円
・1回のトレードでの損失 1万円
・破産ラインを0円ではなく20万円と定義する
この場合は、以下のような式を計算します。
$${\Large 破産確率\ =\ \left(\frac{負ける確率}{勝つ確率} \ \right)^{\frac{資金額\ -\ 撤退ライン\ }{1回あたりの損失\ }}}$$
つまり以下です。
$${\Large 破産確率\ =\ \left(\frac{負ける確率}{勝つ確率} \ \right)^{\frac{100万円\ -\ 20万円\ }{1万円\ }}}$$
要するに、破産のラインを20万円と考えたい(資金が20万円に減る前には撤退したい)という場合は、最初の初期資金を 100万円 – 20万円 = 80万円 で考えればいいだけです。
2.利益と損失の割合が違う場合の公式
もちろん実際のトレードでは、1回の利益と損失の額は同じではありません。そこで、以下のような利益と損失の割合が異なる場合を考えてみましょう。
1)平均利益2万円 / 平均損失1万円
2)平均利益率 3.8% / 平均損失率 1.9%
これはどちらの数字を使っても構いません。さきほども説明したように、どちらにしても「1円ゲーム」に換算して考えるので同じです。つまり、以下のような条件で破産確率を考えます。
1)前提条件
1)損益レシオK = 平均利益 ÷ 平均損失
2)勝ったら K円の利益、負けたら1円の損失というトレード
3)市場の資金は無限と仮定する
4)期待値が0円を超えている
最初の2つのどちらを使っても、損益レシオKは同じになります。
なので、どちらを使っても構いません。
2)「平均利益」と「損益レシオ」に注意
ここでの平均利益を平均リターンと混同しないよう注意してください。一般的にいう平均リターン(期待値)は、すべての平均利益と平均損失を通算した平均値です。一方、ここでいう「平均利益」は、純粋に利益が出た場合のみの平均値です。
また損益レシオとプロフィットファクター(PF)を混同しないでください。PFは「総利益 ÷ 総損失」ですが、この数字にはすでに勝率が含まれています。損益レシオは、勝率とは関係のない数字です。
3)具体的な公式
「1円ゲームに換算するのは同じ」といいましたが、公式はかなり違った姿になります。結論からいうと、この場合の公式は以下になります。
・勝率 P
・損益レシオ k のとき
$$\begin{array}{l}
Px^{k+1} +( 1-P) -x=0\ \ \ を満たすような\\
\ 0< x< 1\ の範囲の\ x\ を\ x=R\ とすると
\end{array}$$
$${\Large 破産確率\ =\ R^{\frac{資金額}{1回あたりの損失} \ }}$$
この記事から読み始めてくださった方は、「いきなり難しそうな方程式が….」と思ったかもしれませんね(笑)
しかし前回の記事を読んでくださった方であれば、何となく見覚えがあるのではないかと思います。この式は、実は前回の記事で出てきた「特性方程式」と(k+1)の部分以外は全く同じです。
注意
なお、上記の公式の「1回あたりの損失額」は、実際のトレードではなかなか定義できません。具体的な損失額はそのときのBTC価格やロット数によって変動するからです。ですが、ここは後ほど説明するので今は気にしないでください。
4)上記の式になる理由
では本当に上記のような公式になるのか確認していきましょう。なお、途中までは前回の記事と全く同じ流れなので、重複する箇所は説明を端折ります。わからない方は、前回の記事を読んでください。
まず、ある資金額n円で破産する確率をQ(n)とします。そして現在の資金額を100円とします。このとき、現在の破産確率 Q(100)は以下のような確率の合計で表すことができます。
1)資金100円で将来的に破産する確率 Q(100)
2)次に勝って資金がn+k円 になり、将来的に破産する確率 P × Q(n+k)
3)次に負けて資金がn-1円 になり、将来的に破産する確率 (1-P) × Q(n-1)
$${\small Q( 100) \ =\ P\times Q( 100-k) \ +\ ( 1-P) \times Q( 100-1) \ }$$
これを前回と同様に一般化して漸化式にします。
(漸化式)
$${\small Q( n) \ =\ P\cdotp Q( n+k) \ +\ ( 1-P) \cdotp Q( n-1) \ }$$
さらに特性方程式を作ります。
(特性方程式)
$${\small \begin{array}{l}
x\ =\ Px^{k+1} +( 1-P)\\
\\
より、Px^{k+1} +( 1-P) -x\ =0\
\end{array}}$$
前回はこの方程式を解くと、たまたま綺麗に解が X=1,(1-P)/P になりました。だから (勝つ確率 ÷ 負ける確率)をベースにした公式になったわけですね。
・前回は特性方程式の解が P(1-P) だったので
$${\large 破産確率\ =\ \left(\frac{1-P}{P}\right)^{資金量\ }}$$
なぜ特性方程式の解からこの式が導き出せるのかは(しつこいですが)前回の記事で長々と説明しているので、そちらを参考にしてください><
全く同じ理由で、この方程式を解いてその解をRとしたときも、「Rの資金乗」が、そのまま破産確率になります。
・上記の特性方程式の解がRのとき、
$${\Large 破産確率\ =\ R^{資金量\ }}$$
4)この方程式の解き方
ただし前回の式は、x の2次方程式だったので、解は2つしかありませんでした。今回はk+1次の方程式なので解は2つとは限りません。そこで、以下のような2つの前提条件を思い出してください。
1)破産確率は、確率の関数である
2)「期待値は0を超えている」という前提がある
Q(n)は、破産する確率を計算する関数です。
確率は0~1までの範囲に必ず収まらなければなりません。そのため、Rは必ず 0≦R≦1の範囲でなければなりません。Rがマイナスの値や1を超える値を取ると、上記の公式では確率が0%を下回ったり、100%を超えてしまうからです。
また「期待値が0を超えている」という条件を満たす場合、解のRは必ず0~1の範囲に1つ存在します。これは色々説明するよりも、実際に上記の方程式をpythonで描画してみた方がイメージが湧きやすいでしょう。
このブログはpythonの実践ブログなので、実際に上記の方程式をpythonで解いてみましょう!
3.Pythonコードで方程式を解こう!
今回は以下のようなBOTの破産確率を考えます。
「1回あたりの損失額」以外は、すべて実際のドンチャン・チャネルブレイクアウトBOTの成績をそのまま使います。
成績
・勝率 41.5%
・平均利益率 8.52%
・平均損失率 2.85%
・損益レシオ 2.99
仮定条件
・初期資金 100万円
・1回の負けトレードの損失額1万円
まずは先ほどの漸化式から導いた特性方程式をpythonで関数にしてみましょう。
#---設定値--- winning_percentage = 0.415 payoff_ratio = 2.99 # 特定方程式の関数 def equation(x): p = winning_percentage k = payoff_ratio return p * x**(k+1) + (1-p) - x
これは先ほどの特性方程式の左辺をそのまま書いただけです。この関数に適当なxの値を渡せば、以下の式の計算結果を返します。
$$Px^{k+1} +( 1-P) -x$$
特性方程式を解くためには、この関数から「0」が返ってくるような0≦x≦1の範囲内のxを探し出せばいいわけです。しかしその前に、本当に0~1の間に解が1つだけ存在するのか、この関数をプロットして確認してみましょう。
2)グラフで描画する
pythonでは、matplotlibというライブラリを使って関数を描画することができます。以下のようなコードを書いて、上記の特性方程式の関数を描画してみましょう。
import matplotlib.pyplot as plt import numpy as np # 設定値 winning_percentage = 0.415 payoff_ratio = 2.99 # 特性方程式の関数 def equation(x): k = payoff_ratio p = winning_percentage return p * x**(k+1) + (1-p) - x # グラフで描画する x = np.linspace(0, 1.2, 100) plt.plot( x,equation(x) ) plt.axhline( y=0,linestyle="dashed" ) plt.axvline( x=1,linestyle="dashed" ) plt.show()
上記のコードでやっていることは、以下です。
1)np.linespace()で、0~1.2の範囲で等間隔な100個の数字を作る
2)それをxとして片っ端から特性方程式の関数に与える
3)返ってきた値をyとして、plt.plot(x,y)をグラフに描画する
つまり0~1.2の範囲の100コの数字をxとし、それに対応する100コの計算結果をyとし、xとyを描画したらグラフの形状がわかるわけです。さらに見やすいように、axvhline()でy=1の水平線、axvline()でx=1の垂直線をセットで描画しています。
では、実行してみましょう!
実行結果

勝率41.5%、損益レシオ2.99 の場合の特性方程式は、上記のような形状になることがわかりました。
この方程式を解くということは、y=0と交わるxを探すということです。ちゃんと0≦x≦1の範囲に、X=1と0<R<1を満たす2つの解が存在していることがわかります。
期待値が0円を下回る場合
では、次に期待値が0円を下回る場合を考えてみましょう。
ちなみに期待値が0を下回るかどうかは、以下のような式を満たすかどうかで確認できます。
$${\large \frac{平均損失率}{平均利益率\ +\ 平均損失率} \ > \ 勝率}$$
これは以下の期待値の計算式を展開すればわかります。気になる方は自身で確認してみてください。
$${\small 1\times 平均利益率\times P\ -\ 1\times 平均損失率\times ( 1-P) < 0}$$
では、以下のような期待値が0を下回るケースを考えてみましょう。
・勝率 31.0%
・平均利益率 8.52%
・平均損失率 3.85%
・損益レシオ 2.21
このケースは、計算してみるとわかりますが、ぎりぎり期待値が0を下回ります。これで特性方程式の関数のグラフの形状を確認してみましょう。
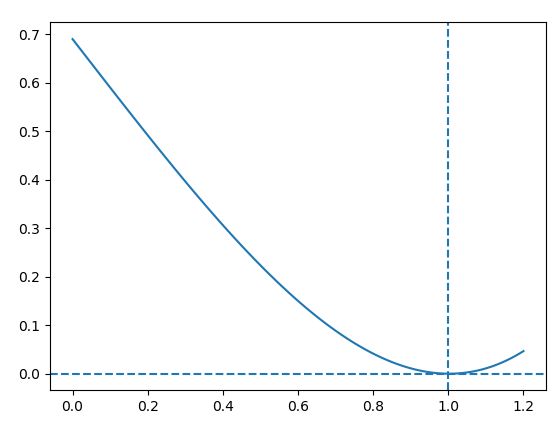
解Rがかなり1に接近して0<R<1の範囲におさまるか怪しくなってきました。実際にこの方程式を解いてみると、解Rは、R=1.0044999 となり、1以下におさまっていません(解き方は後述します)。
では、もっと成績を悪化させてみるとどうでしょうか?
・勝率 28.7%
・平均利益率 8.52%
・平均損失率 4.86%
・損益レシオ 1.75
これは明らかに期待値がマイナスですが、グラフを確認してみましょう。
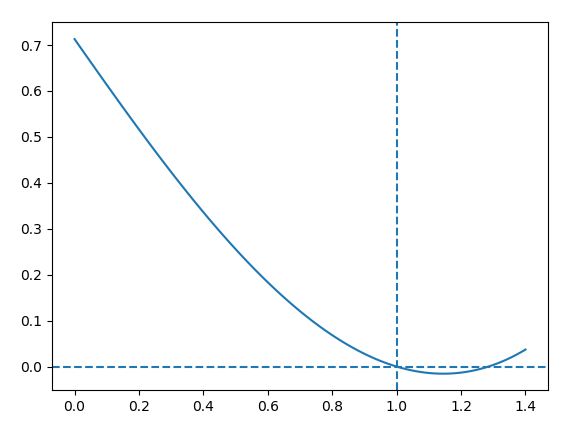
このように解Rは1とは反対側にいってしまい、0<R<1を満たす解Rは存在しないことがわかります。ちなみにこのときの解R=1.2851999です。これで、さきほどの確率の公式に「期待値が0を上回るとき」という条件が付いている理由が理解できたと思います。
特定方程式の意味
これで特性方程式の解が何を意味する数字なのか、少しイメージできたのではないでしょうか?
要するに特定方程式の解Rは、損益レシオと勝率という2つの成績指標を加味して0~1の範囲の数値に換算したものなのです(小さければ小さいほど良い数値で、1を超えると期待値が0円を下回ります)。そこに資金量を乗じることで破産確率が計算できます。
3)方程式を解く
では次に実際に、この特性方程式を解いて破産確率を計算してみましょう!
さきほどのコードに2つほど関数を付け加えます。
import matplotlib.pyplot as plt
import numpy as np
# 設定値
winning_percentage = 0.415
payoff_ratio = 2.99
loss_per_trade = 10000 # トレード1回の損失(仮定)
funds = 1000000
# 特性方程式の関数
def equation(x):
k = payoff_ratio
p = winning_percentage
return p * x**(k+1) + (1-p) - x
# 特定方程式の解を探す
def solve_equation():
R = 0
while equation(R) > 0:
R += 1e-4
if R>=1:
print("期待値が0を下回っています")
R=1
print("特性方程式の解は{}です".format(R))
return R
# 破産確率を計算する公式
def calculate_ruin_rate( R ):
e = funds / loss_per_trade
return R ** e
pythonのようなプログラムが方程式を解く場合、人間のように因数分解や微分をしてスマートに解くよりも、ゴリゴリと片っ端から数字を代入しまくって近い数字を探すほうが得意です。
特に今回のように、解が0<R<1の範囲とわかっているような場合は尚更です。そのため上記のプログラムでは、0から順番に0.0001単位で数字を代入しまくって、最もy=0に近い数を返すようにしています。
このときのxは、ピッタリ厳密なy=0ではありませんが、どのみち、実際にトレードで何らかの指標として使う際には四捨五入しますので、近似値で問題ありません。無理数(ルートなど)で答えを返されても使えないからです。
▽ 解を探す箇所
R = 0 while equation(R) > 0: R += 1e-4 #「1e-4」は「0.0001」と同じ意味
さきほどの説明の通り、0≦x≦1 の範囲に必ず解は存在することがわかっています。そのため、0からスタートして +0.0001 ずつ加算していき、計算結(y)が0を下回った時点でループを止めます。
もし期待値が0を下回っている場合は、解Rに辿り着くよりも前に x=1 にぶつかります。そのときは「期待値が0以下です」と表示して、R=1 を返します。
※ R=1 のときの破産確率は必ず100%です。1は何乗してもずっと1だからです。
実行結果
では以下のようなメイン処理を書いて実行してみましょう!
今度は確認のために、解Rもグラフ上にプロットしてみます。
# メイン処理
R = solve_equation()
ruin_rate = calculate_ruin_rate(R)
print("破産確率は{}%です".format( round(ruin_rate * 100,2) ))
最初の勝率・損益レシオの条件では以下のような結果になりました。
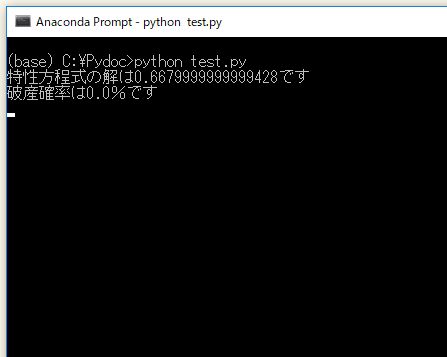
破産確率は0%です。
念のため、以下のようなコードを追記して解Rが正しいかどうかグラフにプロットしてみましょう。
# グラフを描画 x = np.linspace(0, 1.2, 100) plt.plot( x,equation(x) ) plt.axhline( y=0,linestyle="dashed" ) plt.axvline( x=1,linestyle="dashed" ) plt.axvline( R, color="gray" ) plt.show()
以下のグレーの線が、x=Rの位置を垂直線でプロットしたものです。ちゃんと正しい箇所を求めることができています。
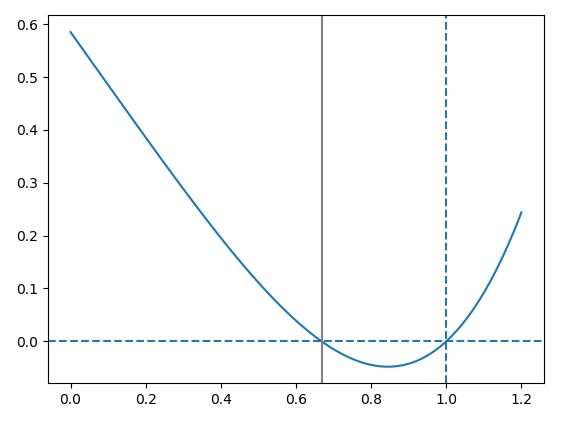
資金の条件を変えてみた場合
ではBOTの成績は同じまま、初期資金を10万円に変えてテストしてみましょう。
成績
・勝率 41.5%
・平均利益率 8.52%
・平均損失率 2.85%
・損益レシオ 2.99
仮定条件
・初期資金 10万円
・1回の負けトレードの損失額1万円
この場合の破産確率は以下のようになります。
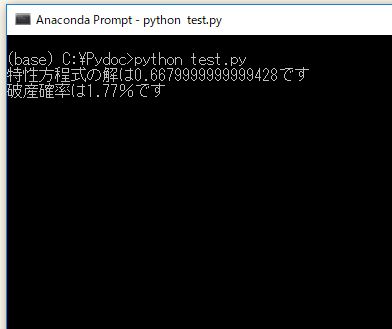
特性方程式の解Rは変わっていませんが、破産確率は 1.77%に上昇しています。
同じように1回の負けトレードの損失額(=1回の賭け金)を上げた場合も、破産確率は上昇します。全く同じ損益レシオや勝率のBOTを使っても、初期資金や毎回のトレードで取るリスク額によって、破産確率が変動することがわかります。
これが前回の記事で、「損益レシオと勝率だけのバルサラ破産確率表を使ってもあまり意味がない」と説明した理由です。
次回
さて、今回はより実践的なトレードで「平均利益と平均損失の割合が異なる場合」の破産確率の計算方法を解説しました!
しかし残念ながら、あと1つだけどうしても簡単に設定できない数値があります。それが「1回の負けトレードの損失額」(=賭け金)です。
1)1回の損失額の定義
トレードにおける賭け金とは、この記事の定義でも確認したように1回のトレードで実際に損する金額のことです。しかし実践のトレードでは、この「1回のトレードの損失額」は一定額に固定することができません。
例えば、第7回の「資金管理編」では、毎回、口座残高のX%だけリスクを取り、そのリスクの範囲内でポジションサイズを計算する方法を紹介しました。この方法の場合、毎回の賭け金(トレードでリスクに晒す金額)は、そのときの口座残高に応じて毎回変動します。
「毎回1万円を賭ける」と決まっているゲームであれば、上記の公式をそのまま使うことができます。ですが、トレードのように毎回の損失額を固定できないゲームでは、上記の公式を使って破産確率を計算することはできません。
2)対数(log)に変換する
最後の検証で確認したように、上記の公式の「1回のトレードの損失額」は、それ自体が破産確率に影響します。そのため、平均損失率(%)などの割合ではなく、何らかの具体的な金額(絶対値)を使わなければなりません。
しかしこれを割合で置き換える方法が1つあります。それが、初期資金や損失額などのお金の単位を「円」ではなく「log(対数)」に変換する方法です。この方法を使えば、「毎回のトレードで口座の一定率(3%等)のリスクを取った場合」などの破産確率をシミュレーションできるようになります。
次回の記事は、高校数学のlogを忘れた方でもわかるように、これについて詳しく解説します。