ある勝率と期待値をもつBOTが、実際にある一定期間でどのくらいの運用成績を得られるか?を判断するのは非常に難しい問題です。とくに定額ではなく定率(複利)でトレードをする場合、なおさら予測は困難になります。
例えば、ある売買ロジックでBOTを運用した結果、1年間で以下のような結果が得られたとします。実成績でもバックテストの結果でも構いません。
(例)
期間:2018/5/19~2019/5/19
全トレード数 161回
勝率 20.5%
平均利回り 1.06%
平均利益率 10.2%
平均損失率 -1.3%
———————————–
運用パフォーマンス
———————————–
初期資金 : 500000円
最終資金 : 1948155円
運用成績 : 390.0%
手数料合計 : -273098円
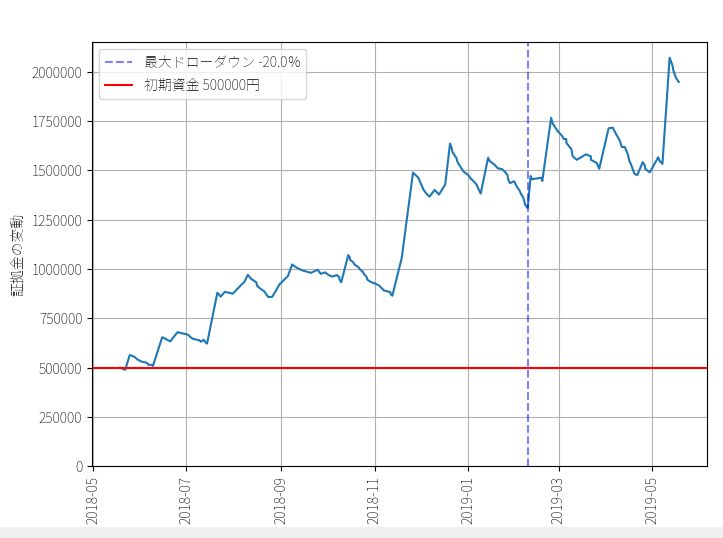
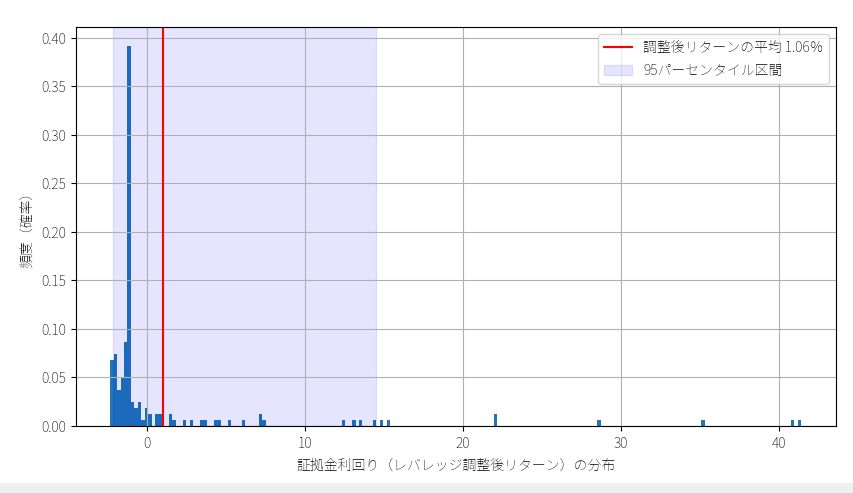
これは実際にあるパラメータで1時間足のチャネルブレイクアウトBOTを(口座のリスク率2%)で動かした場合の運用成績の例です。
疑問
この結果だけを見ると最終成績は良好に見えます。1年間で3倍以上になっていますから。しかし問題なのは、『この最終成績390%という数字はどの程度、運が良かった結果なのか?』という情報が、最終成績の数字を見てもよくわからない点にあります。
仮に勝率20.5%、期待値1.06%(平均利益10%、平均損失-1.3%)という結果の元となる確率分布が、今後も続くと信じることを前提にしても、161回の試行で390%という運用成績が果たしてどのくらい「ありうる」ことなのか? かなり運が良かったのか、それとも期待値通りの平凡な結果だったのか、潜在的にどのくらいドローダウンリスクがあったのか? この数字だけではわかりません。
今回の記事では、判断の目安として、得られたリターンのサンプルから何度も復元抽出(リサンプリング)をして、ありえた最終成績のシミュレーションをするブートストラップ法を紹介します。
ブートストラップ法(復元抽出)
ブートストラップ法とは、1度だけしか抽出できないサンプルを再利用して大量のトレード結果を疑似的に生成するモンテカルロシミュレーションです。数学が得意でないので、厳密な定義はわかりませんが、多分そんな感じです。
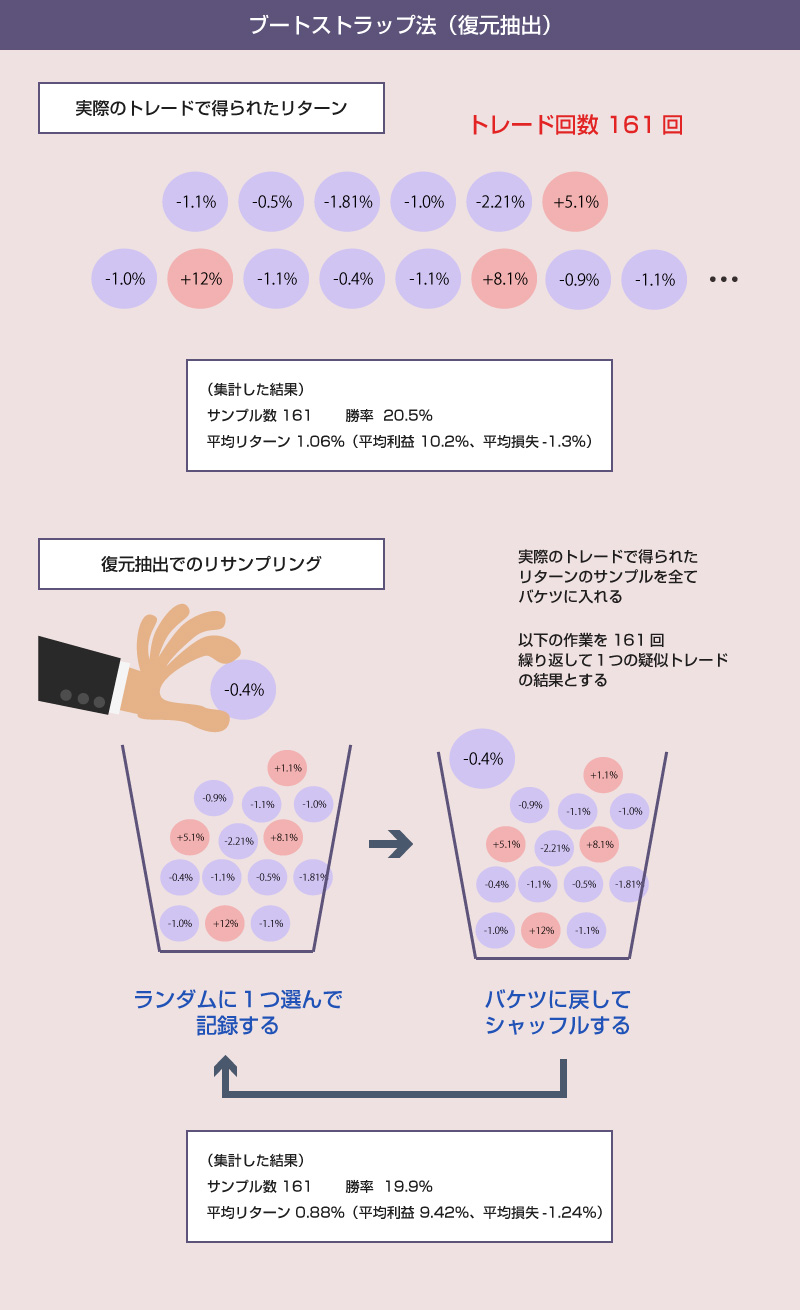
この方法の優れたところは、リターンがどんな確率分布に従うのかわからない(正規分布などでモデル化できない)場合でも、実際のサンプルから好きなだけ疑似的なトレード結果を生成できることです。
復元抽出(=1度選んだ玉をバケツに戻す方式)なので、実際にありえる値の中から実際にありえる頻度(確率)に近い形でリターンを選んで、それを使って異なる結果をシミュレーションすることができます。
もちろん同じサンプルを何度も使ってるだけなので、何万回も試行を繰り返せば同じ分布になります。ですが、1年間の成績(161回のトレード)という少ない試行回数の制限の中では、どの程度、結果がバラつく可能性があったかをシミュレーションできます。
pythonコード
ブートストラップ法のイメージを掴むために、疑似的なトレード結果のサンプルを合計25セットほど作成してその結果をグラフにしてみましょう。
▽ 実際のトレードで得られたリターンのサンプル161個

▽ csvファイルに集計
-2.135,15.292,-1.133,-1.02,-1.843,-2.156,-0.794,-1.107,-1.083,-0.031,-1.068,28.578,-1.034,-1.547,-0.599,7.268,-1.419,-0.417,-2.124,-1.076,-1.109,-1.172,1.587,-1.981,-1.087,41.402,-1.122,-1.09,2.864,-1.089,7.148,3.553,-2.005,-1.972,-2.023,-1.865,-1.085,-1.092,-1.096,-1.079,0.169,7.34,4.487,6.202,-1.068,-1.079,-0.852,-1.234,1.611,-2.103,0.805,-1.13,-1.084,0.782,-1.286,-1.215,-1.285,14.745,-1.112,-1.074,-1.17,-1.251,-1.133,-1.258,-1.3,-1.219,-1.54,-1.213,-1.296,-0.761,-1.169,-1.176,-1.507,-0.509,-0.538,-1.212,-0.798,22.072,40.899,-1.802,-1.051,-2.005,-1.056,-1.574,-1.059,2.483,-1.657,3.692,14.52,-1.598,-1.039,-2.046,-1.062,-1.394,-1.955,-1.13,-1.038,-1.106,-1.077,-1.216,-2.013,13.119,-1.114,-1.134,-1.178,-0.287,-1.059,-1.112,-1.151,-1.501,0.696,-2.151,-1.174,-1.236,-1.319,-1.206,-1.496,-1.202,12.396,-1.14,0.541,-1.133,22.143,-1.593,-2.306,-1.196,-1.131,0.01,-1.16,-2.036,-2.2,-1.103,1.774,-0.634,-1.143,-0.973,-1.93,13.559,0.187,-1.796,-1.816,-2.214,-0.033,-2.169,-2.207,-1.051,-1.095,-2.146,-0.44,4.444,-1.131,-1.112,-1.134,5.13,-1.066,-1.092,35.116,-2.012,-1.027,-2.018,-0.996
まずは上記のように、実際のトレードまたはバックテストで得られたリターンの結果(161個)を羅列して1つのcsvに保存します。ここでは仮に return.csv で保存したとします。
次に以下のようなコードをpythonファイルで保存して、読み込みます。
▽ pythonコード
from matplotlib import pyplot as plt
import numpy as np
import random
#------------------------------------
import matplotlib as mpl
font = {"family":"Noto Sans CJK JP"}
mpl.rc("font",**font)
#-------------------------------------
#----------------------------------------------------
# 準備
#----------------------------------------------------
data = np.genfromtxt("./return.csv",delimiter=",")
trade_N = 161
N = 25
random_return = np.zeros((N,trade_N))
av_av_return = np.zeros(N)
# 資産推移の行列
asset_simulation = np.zeros((N+1,trade_N+1))
start_funds = 500000
asset_simulation[:,0] = start_funds
for i in range(trade_N) : asset_simulation[0][1+i] = round(asset_simulation[0][i] * (data[i]/100+1))
#----------------------------------------------------
# 使う関数
#----------------------------------------------------
# 勝率の計算
def winrate( data ):
r = np.sum( data>0 ) / data.size
r = round(r*100,1)
return r
# 平均リターンの計算
def av_return( data ):
r = data.mean()
r = round(r,2)
return r
# 勝ちの平均利益と負けの平均利益を計算
def win_lose_rate( data ):
win_r = np.where( data>0, data, 0 )
win_r = round( win_r.sum() / np.sum(data>0) ,2 )
lose_r = np.where( data<0, data, 0 )
lose_r = round( lose_r.sum() / np.sum(data<0) ,2 )
return win_r,lose_r
# ブートストラップのグラフを表示する関数
def hist_return( data,i ):
plt.subplot(5,5,i)
n1,n2 = np.histogram( data, bins=200 )
average = round(data.mean(),2)
percentile_5 = np.percentile( data,5 )
percentile_95 = np.percentile( data,95 )
y = n1/float(n1.sum())
x = (n2[1:]+n2[:-1])/2
x_width = n2[1] - n2[0]
plt.bar( x, y, width=x_width )
plt.axvline( average, color="red", label="平均リターン {}%".format(average) )
plt.axvspan( percentile_5, percentile_95, color="blue",alpha=0.1, label="95パーセンタイル区間")
plt.grid()
plt.legend()
#----------------------------------------------------
# リサンプリングの結果を表示してグラフ化
#----------------------------------------------------
for i in range(N):
print("----------------------")
random_return[i] = np.array( random.choices( data, k=trade_N )) # 復元抽出
for k in range(trade_N) : asset_simulation[i+1][k+1] = round(asset_simulation[i+1][k] * (random_return[i][k]/100+1)) # 資産推移の計算
print("勝率 : {}% ".format( winrate(random_return[i]) ))
print("平均リターン : {}% ".format( av_return(random_return[i]) ))
win_r, lose_r = win_lose_rate( random_return[i] )
print("平均利益率 : {}% ".format( win_r ))
print("平均損失率 : {}% ".format( lose_r ))
av_av_return[i] = av_return(random_return[i])
hist_return(random_return[i],i+1)
plt.title("リターンの分布と頻度")
plt.show()
#----------------------------------------------------
# リサンプリングで得られた平均リターンのヒスグラム
#----------------------------------------------------
n1,n2 = np.histogram( av_av_return, bins=200 )
average = round( av_av_return.mean(),2)
percentile_5 = np.percentile( av_av_return,5 )
percentile_95 = np.percentile( av_av_return,95 )
y = n1/float(n1.sum())
x = (n2[1:]+n2[:-1])/2
x_width = n2[1] - n2[0]
plt.bar( x, y, width=x_width )
plt.axvline( average, color="red", label="平均リターンの平均値 {}%".format(average) )
plt.axvspan( percentile_5, percentile_95, color="blue",alpha=0.1, label="95パーセンタイル区間")
plt.grid()
plt.xlabel("復元抽出した平均リターンの分布")
plt.ylabel("頻度")
plt.legend()
plt.show()
上記のコードは、ブートストラップ法によって生成した疑似トレード161回の結果を合計25セット生成し、その勝率、平均リターン、ヒストグラムを図にするコードです。
trade_N が1セットあたりのトレード回数(=実際のトレードやバックテストで集計されたトレード回数)です。それを1セットとします。 N はブートストラップ法で何セット疑似サンプルを生成するかを指定する数字です。
ここでは5×5で綺麗に図にしたかったので25セットにしましたが、何セットでも構いません。欲しいだけいくらでもデータを生成できます。実際、あとで10万セット生成して運用パフォーマンスをシミュレーションする例を紹介します。
実行結果
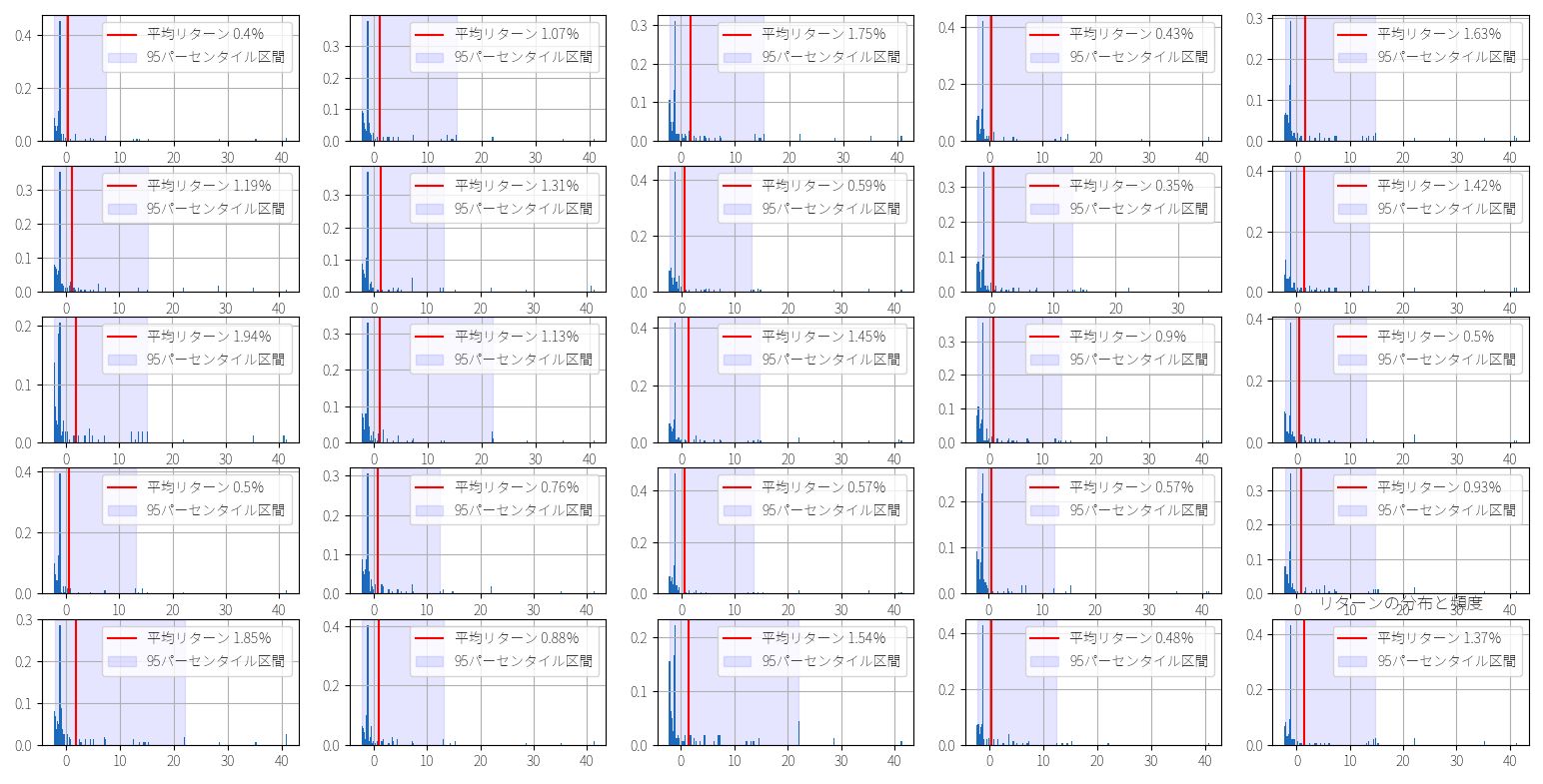
このように25セットの疑似データを生成することができました。同じサンプル(実際のトレード結果)から再抽出してるので、どれもパッと見では似たようなリターン分布になっています。左上の4個を拡大したものが以下です。
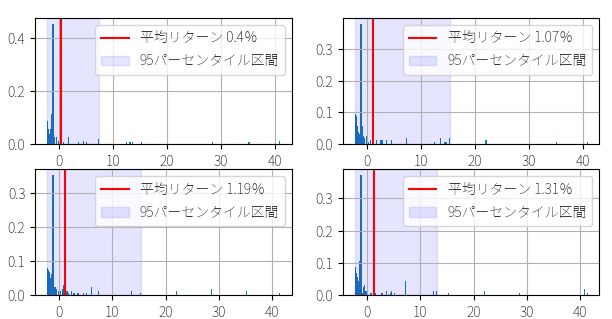
しかし実際には、以下の出力を見るとわかるように、勝率には13.7%~27.3%まで大きなバラつきがあり、結果として1トレード当たりの平均リターンも 0.48%~1.94%まで大きなバラつきがあります。
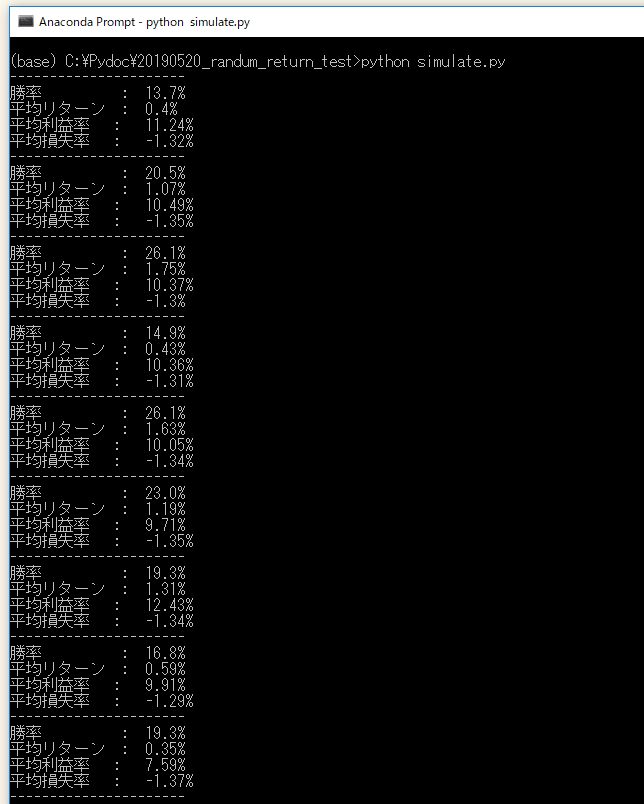
以下は 疑似生成した25セットのトレード結果の平均リターンをヒストグラムにしたものです。赤い線は、161回のトレードの平均リターンを25回採取したものの平均値(=つまり平均リターンの平均)です。
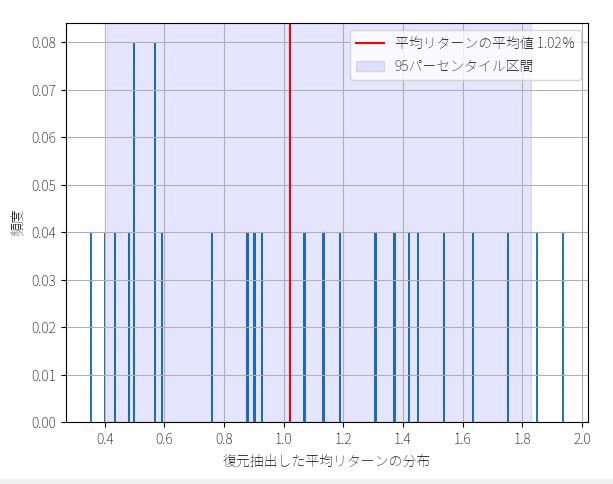
このように25回ほどシミュレーションを繰り返してみた結果、大体どの場合でも平均リターンは一応プラスになりそうだということ、年間161回という少ない試行の中では、運が悪ければ勝率が13%程度ということもありえた、ということ、などが想像できます。
25回のシミュレーションでは、1番低い平均リターンは +0.35%でした。
資産カーブをグラフ化する
それでは次に、いよいよ知りたかった「最終的な運用パフォーマンスにどのくらいのバラつきがありえたのか?」を検証してみましょう。ブートストラップ法で疑似的に生成したトレード結果を最初の資金に適用して、最終資金のシミュレーションをします。
なお注意点として、ここで用いる「リターン」のサンプルが、証拠金利回りの数字になっていることを確認してください。この数字を用いないと、初期資金とリターンを掛け合わせた結果が最終的な資金と一致しません。
単なるリターンと証拠金利回りの違いはこちらの記事で解説しています。
▽ pythonコード
#----------------------------------------------------
# 資産カーブのグラフ化
#----------------------------------------------------
plt.grid()
for i in range(N): plt.plot( asset_simulation[i+1] )
plt.ylim(ymin=0)
plt.axhline( start_funds, color="#2e8b57", label="初期資金 {}円".format(start_funds) )
plt.plot( asset_simulation[0], color="black", lw=5, label="最初の資産カーブ" )
plt.legend()
plt.show()
これを実行すると以下のようになります。
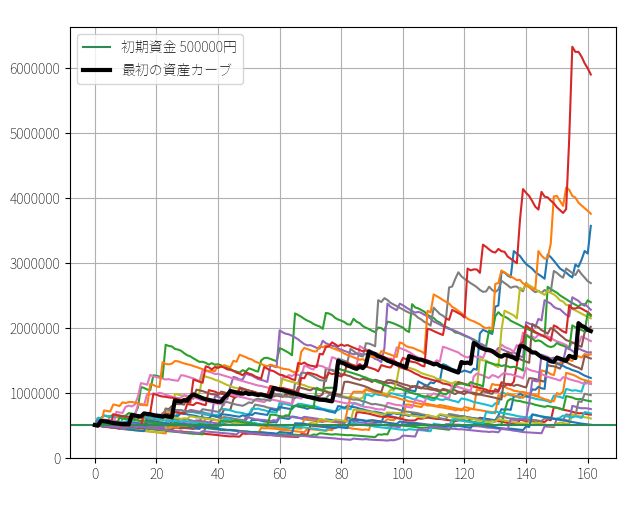
「太い黒線」が実際のトレード(バックテスト)で得られた資産カーブです。たった25回のシミュレーション結果を見るだけでも、最終資金は、50万円~300万円以上まで幅広くバラついているのがわかります。運が悪ければ、ほとんど資産が増えなかったケースもあり得たかもしれません。
ちなみに1000回ほどシミュレーションすると以下のようになります。
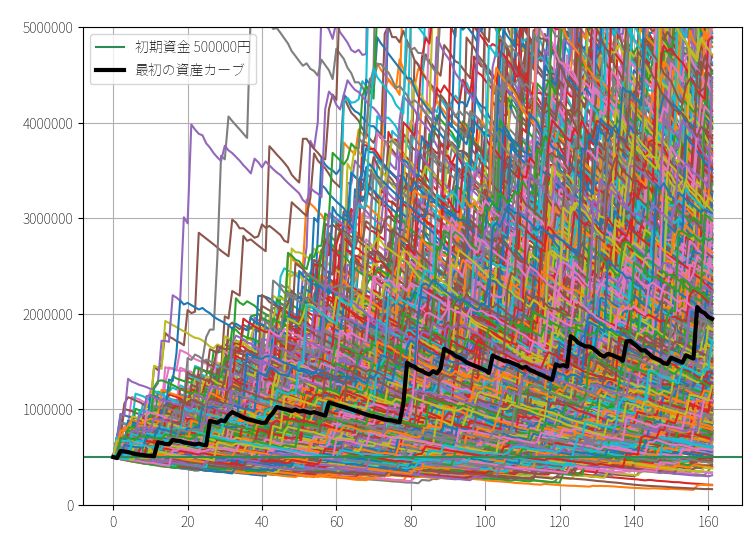
10万回シミュレーションする
上記のグラフを見ても、「どのくらいの最終資金になる可能性が高いのか?」「最終資金が50万円(初期資金)を下回る可能性はどのくらいあるのか?」いまいちわかりません。なので、ブートストラップ法で10万回ほど疑似トレード結果をシミュレーションして最終資金のヒストグラムを作りましょう。
▽ pythonコード
#----------------------------------------------------
# 最終資金のヒストグラム
#----------------------------------------------------
last_funds = asset_simulation[:,-1]
median = np.median( last_funds )
n1,n2 = np.histogram( last_funds, bins=1000 )
percentile_5 = np.percentile( last_funds,5 )
percentile_95 = np.percentile( last_funds,95 )
y = n1/float(n1.sum())
x = (n2[1:]+n2[:-1])/2
x_width = n2[1] - n2[0]
mode = round(x[np.argmax(y)])
plt.bar( x, y, width=x_width )
plt.axvline( mode, color="red", label="最終資金の最頻値 {}円".format(mode) )
plt.axvspan( percentile_5, percentile_95, color="blue",alpha=0.2, label="95パーセンタイル区間" )
plt.axvline( percentile_5, color="blue", label="5パーセンタイル値 {}円".format( round(percentile_5)) )
plt.axvline( median, color="black", linestyle="--",label="中央値 {}円".format(round(median)) )
plt.grid()
plt.xlabel("ブートストラップ法による最終資金の分布(単位:円)")
plt.ylabel("確率")
plt.xlim(0,last_funds[0]*3)
plt.xticks(rotation=90)
plt.legend()
plt.show()
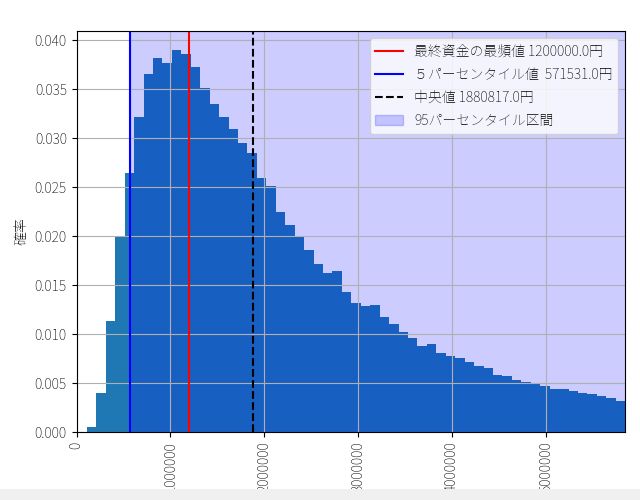
5パーセンタイル値 : 57万1531円(運用成績 114.3%)
最終資金の最頻値 : 120万0000円(運用成績 240.0%)
中央値 : 188万0817円(運用成績 376.1%)
実際の成績は194万円(390)%でしたが、これだけ勝率が低くかつ利益のバラつきが大きい売買ロジックでは、最終資金が120万円(最頻値)~190万円(中央値)くらいに終わってもおかしくなかったことがわかります。ただし相当運が悪くても初期資金50万円を割る可能性は5%以下とかなり低いようです。
▽ ありえた「平均リターン」の分布

トレンドフォロー戦略のBOTの場合、そもそも1トレードあたりの勝率が低く、かつ利益が出た場合のバラつきが極端に大きいので、「実際の成績よりも利益が増えた場合」のシミュレーション結果には、ほとんど意味がありません。
中には最終資金が1000万円を超えるようなシミュレーションもありますが、それは単に勝ちトレードのサンプル数が少ないことが原因です。復元抽出なので、10万回もテストすれば極端に高い利益を何度も選びなおす可能性もあります。 当然ですが、実際に市場でそのような利益機会が生じた可能性を意味するわけではありません。
一方、「実際の成績よりも悪かった場合」のシミュレーションはそれなりに信憑性があると思います。
もちろん市場の過去データは1通りしかないので、何度サンプルを取り直したところで本当の意味で複数のシミュレーションをすることはできません。しかし負けトレードの結果はサンプル数も多く分散も小さいので、現実にありえない値を取る可能性は低く、本当の勝率が想定より低かった場合をうまくシミュレーションできます。
また同時に、極端に1回だけ高い利益が出たことで全体の成績が実際より良く見えている場合(外れ値の影響)は、ブートストラップ法で何度もリターンを復元抽出することで、その影響を弱めることができます。
補足:数学的にわかること
上記のような最終資金のモンテカルロシミュレーションの意味を、もう少し一般的に理解するために、少し数学的に考えてみましょう。トレードの成績をもっとシンプルに、(1)勝率、(2)勝ったときの平均利益、(3)負けたときの平均損失、の3つのパラメーターだけで決まる確率変数と仮定します。
すると最終資金は以下のように決まります。

つまり最終資金は、勝ちトレードの回数によって決まる関数です。この「勝ちトレードの回数」は、勝率pによって決まる確率変数なので、数学的には以下のような二項分布でモデル化できます。

二項分布という確率分布は、試行回数(N)が十分に大きいとき(勝率が極端に小さくなければ)、正規分布に近似できることが知られています。(参考wikipedia)
ということは、最初の式に戻ってみると、「勝ち回数」を表す指数の部分(x乗)は正規分布で近似できることがわかります。 指数のところが正規分布に従うような確率変数を、対数正規分布といいます。
対数正規分布というのは、トレードをしている方の多くが聞いたことがあると思いますが、0を閾値として右側にファットテールになる、以下のような形の確率分布です。
▽ 適当な対数正規分布
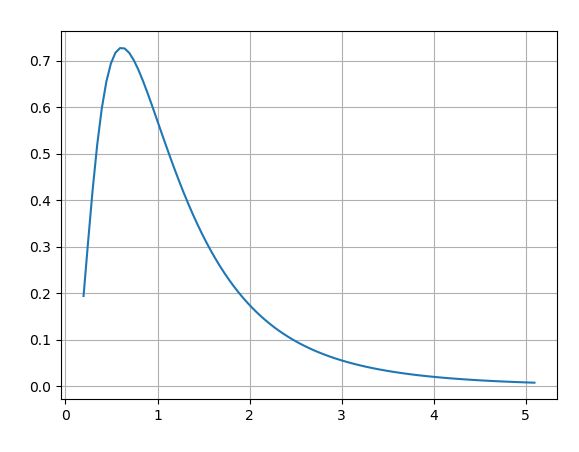
import scipy.stats as stats from matplotlib import pyplot as plt import numpy as np s = 0.7 plt.grid() x = np.linspace( stats.lognorm.ppf(0.01,s), stats.lognorm.ppf(0.99,s), 100 ) plt.plot(x, stats.lognorm.pdf(x,s)) plt.show()
さきほどの最終資金のヒストグラムに似ていますね。
このような確率分布の特徴として、最頻値や中央値が平均値よりも小さくなる(左側に偏る)という性質があります。いわゆる「数少ない一部の人が大勝ちし大半の人は平均より低い成績に偏る」という分布で、年収の分布などと同じです。

つまり、運用するBOTがどのような勝率・期待利益・期待損失を持ってるかに関わらず、基本的には最終資金のグラフの形はこのような感じになる、ということです。なのでグラフの形状自体に意味はありません。どのような売買ルールを採用しても多分こうなります。
有益な情報
ではこのブートストラップ法による最終資金のモンテカルロシミュレーションから、どのような情報を得ればいいのでしょうか。1つは「最終資金のバラつきがどのくらい大きいか?」です。
例えば、同じモンテカルロシミュレーションで、勝率50%、期待利益2%、期待損失1%のBOTの運用をシミュレーションしてみましょう。すると最終資金は以下のようになります。
▽ 初期資金50万円 トレード回数161回
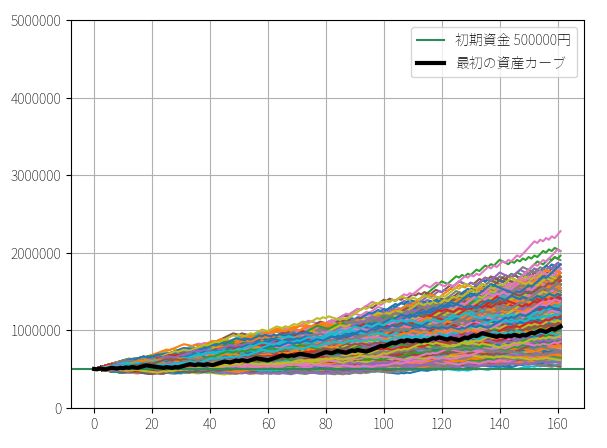
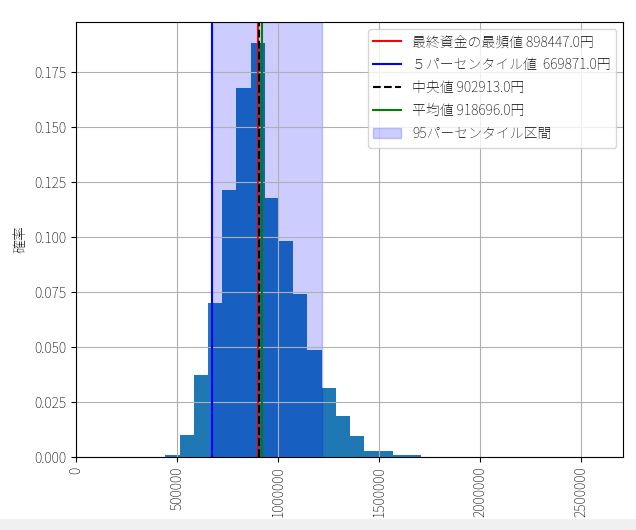
たしかに僅かに右側に偏った分布になっており、最頻値<中央値<平均値のかたちになっていますが、その差はほとんどありません。このような分布であれば、最終的な資金(運用成績)についてある程度の精度で確信を持つことができそうです。
最頻値 89万8447円
中央値 90万2913円
期待値 91万8696円
次にもっと極端な 勝率10%、期待利益14%、期待損失1%のBOTを考えてみます。こちらのBOTも期待リターンは同じ(+0.5%)ですが、最終資金のヒストグラムはもっと歪んだ形になることが予想できます。
▽ 初期資金50万円 トレード回数161回
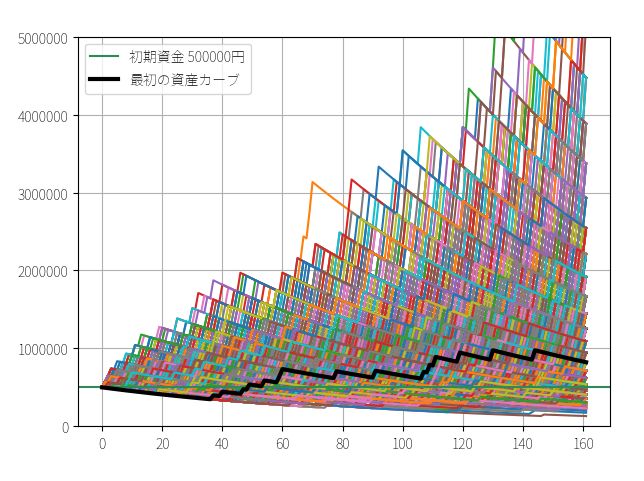
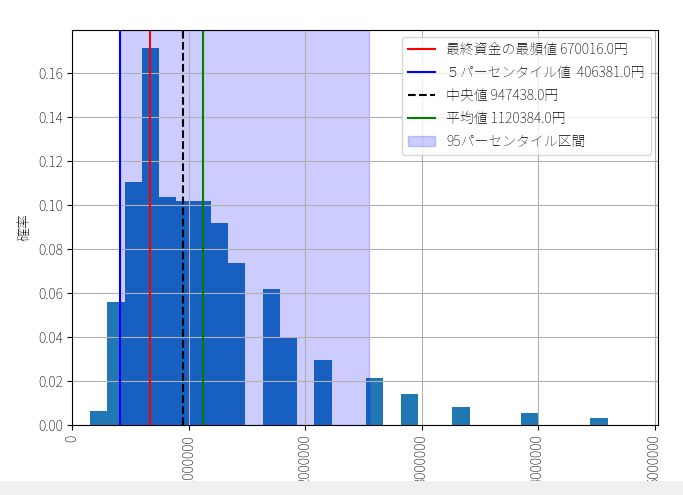
先程のBOTと1トレード当たりの平均リターンは全く同じにもかかわらず、最終資金の分布は大きくバラつき、ハッキリと勝ち組と負け組に分かれてしまっています。中央値はあまり変わりませんが、最頻値はさきほどより遥かに低くなっています。一方で期待値はかなり大きくなっています。
またさきほどの分布とは異なり、5パーセンタイル値が40万6381円で原資割れしています。これは運が悪ければ、初期資金を下回る可能性もあったことを示しています。
最頻値 67万0016円
中央値 94万7437円
期待値 112万0384円
最後のシミュレーションには以下のコードを作りました。
#--------------------------- # トレード結果ジェネレーター #--------------------------- p = 0.1 av_win = 10 av_lose = -1 trade_N = 161 def generate_data( p,N,av_win,av_lose ): data = stats.bernoulli.rvs( p, size=N ) data = [ av_lose if i==0 else av_win for i in data ] return data