前回の記事では、実際に得られたトレード結果からランダムにリターンを復元抽出し、疑似的なトレード結果を生成することで最終資金(運用成績)のバラつきをシミュレーションするブートストラップ法について解説しました。
今回はその続きで、定額トレードで運用した場合と定率トレードで運用した場合の最終資金をモンテカルロシミュレーションで比較し、どのくらい結果のバラつきに違いがあるかを調べてみようと思います。
準備
前回の記事に引き続き、2018/5/19 ~2019/5/19(執筆時)の1年間のデータを使って検証します。手法は1時間足のチャネルブレイクアウトでトレンドフィルターのみ有効にしたものを利用します。
(例)
期間:2018/5/19~2019/5/19
手法:1時間足n期間チャネルブレイクアウト
損切り、トレンドフィルターあり
初期資金 50万円
レバレッジ3倍まで
1.固定額トレード
固定額トレードでは、1トレードあたり100万円分のBTCを売買します。 資金量の変動に関わらずレバレッジをかけて一定額(100万円)でトレードし続けます。ただし原資が33万円を割って100万円の売買ができなくなったら終了です。
初期資金 50万円
レバレッジ 3倍
1トレードの売買額 100万円
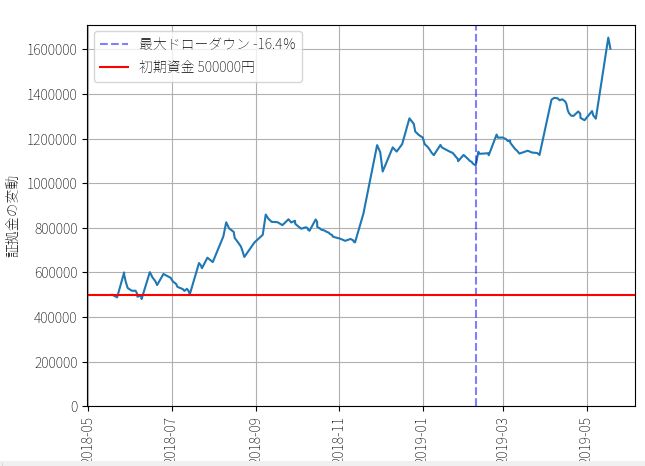
▽ 結果
----------------------------------- 総合の成績 ----------------------------------- 全トレード数 : 148回 勝率 : 25.0% 平均リターン : 0.75% 標準偏差 : 5.58% 平均利益率 : 6.99% 平均損失率 : -1.33% 平均保有期間 : 34.2足分 損切りの回数 : 102回 最大の勝ちトレード : 363183円 最大の負けトレード : -52674円 最大連敗回数 : 14回 最大ドローダウン : -211127円 / -16.4% 利益合計 : 2575531円 損失合計 : -1473109円 最終損益 : 1102422円 スリッページ合計 : -147674円 ProfitFactor : 1.748 ----------------------------------- 証拠金1に対する賭額の割合 ----------------------------------- 平均の賭け率 : 1.18 勝ちトレードの賭け率 : 1.231 負けトレードの賭け率 : 1.162 証拠金に対する平均利回り : 0.97% 平均利益率 : 8.49% 平均損失率 : -1.53% 賭け率とリターンの相関 : 0.04 帰無仮説の確率p値 : 0.62 ----------------------------------- 運用パフォーマンス ----------------------------------- 初期資金 : 500000円 最終資金 : 1602422円 運用成績 : 320.0% 手数料合計 : -147674円
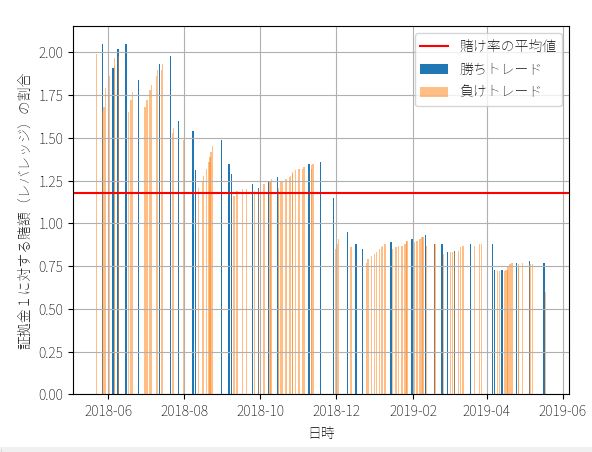
最大レバレッジは3倍ですが、資金が増えるにつれてレバレッジをかける必要がなくなるので、後半で資金効率が落ちてます。最終的な資金効率としては、1回のトレードで平均して1.18倍のレバレッジをかけ、証拠金に対して0.97%の利回りを得ていたことがわかります。利益合計は110万2422円、運用パフォーマンスは320%です。
2.定率トレード
定率トレードでは、常に口座残高の2%のリスクを取ってトレードします。この具体的な意味は、口座残高の2%を損切り幅で割って取得するポジションサイズ(枚数)を決定する、という意味です。詳しくはこちらの記事で解説しています。
資金が増えれば増えるほど取得できるポジションサイズが大きくなるため、いわゆる複利運用にあたります。
初期資金 50万円
レバレッジ 3倍
口座のリスク率 2%
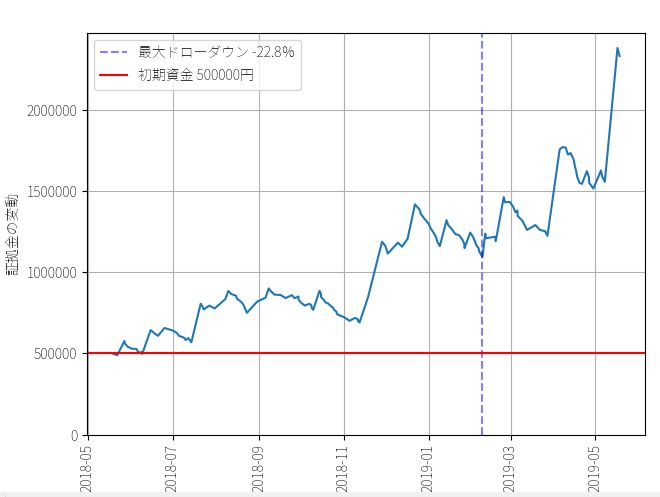
▽ 結果
----------------------------------- 総合の成績 ----------------------------------- 全トレード数 : 148回 勝率 : 25.0% 平均リターン : 0.75% 標準偏差 : 5.58% 平均利益率 : 6.99% 平均損失率 : -1.33% 平均保有期間 : 34.2足分 損切りの回数 : 102回 最大の勝ちトレード : 824328円 最大の負けトレード : -49245円 最大連敗回数 : 14回 最大ドローダウン : -323097円 / -22.8% 利益合計 : 4107175円 損失合計 : -2274386円 最終損益 : 1832789円 スリッページ合計 : -284594円 ProfitFactor : 1.806 ----------------------------------- 証拠金1に対する賭額の割合 ----------------------------------- 平均の賭け率 : 1.879 勝ちトレードの賭け率 : 1.778 負けトレードの賭け率 : 1.912 証拠金に対する平均利回り : 1.38% 平均利益率 : 11.37% 平均損失率 : -1.95% 賭け率とリターンの相関 : -0.01 帰無仮説の確率p値 : 0.93 ----------------------------------- 運用パフォーマンス ----------------------------------- 初期資金 : 500000円 最終資金 : 2332789円 運用成績 : 467.0% 手数料合計 : -284594円
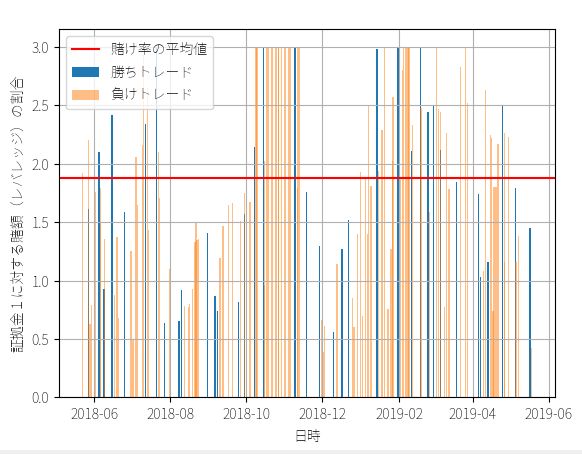
当然ですが、固定額トレードと定率トレードは全く同じ場面でエントリーして損切りや手仕舞いをしています。そのため、トレード回数や勝率、賭け金に対する平均リターンなどの数字は全て同じです。
一方、定率トレードは複利運用をしているので、同じリターンでも証拠金に対する利回り(資金効率)が違います。上の図を見てわかるように、定率トレードは資金が増えたあとも資金効率(レバレッジの比率)が変わっておらず、平均して1回のトレードで1.879倍のレバレッジをかけています。この差が最終成績の違いとして現れています。最終利益は183万2789円、運用成績は467%です。
この違いは、以下の「10%を超えるリターン」の利回りを比較するとわかりやすいです。
▽ 定額トレード 10%を超えるリターン
------------------------------------------ +10%を超えるトレードの回数 : 10回 ------------------------------------------ 2018-05-27 07:00:00 | 11.16% (証拠金利回り 22.88%) | SELL 2018-06-15 03:00:00 | 12.18% (証拠金利回り 24.97%) | SELL 2018-07-21 03:00:00 | 13.97% (証拠金利回り 27.66%) | BUY 2018-08-07 23:00:00 | 11.54% (証拠金利回り 17.77%) | SELL 2018-11-18 12:00:00 | 12.83% (証拠金利回り 17.45%) | SELL 2018-11-28 13:00:00 | 30.90% (証拠金利回り 35.54%) | SELL 2018-12-10 00:00:00 | 10.84% (証拠金利回り 10.29%) | SELL 2018-12-22 05:00:00 | 11.55% (証拠金利回り 09.82%) | BUY 2019-04-05 06:00:00 | 25.02% (証拠金利回り 22.02%) | BUY 2019-05-16 20:00:00 | 36.51% (証拠金利回り 28.11%) | BUY ------------------------------------------
▽ 定率トレード 10%を超えるリターン
------------------------------------------ +10%を超えるトレードの回数 : 10回 ------------------------------------------ 2018-05-27 07:00:00 | 11.16% (証拠金利回り 17.97%) | SELL 2018-06-15 03:00:00 | 12.18% (証拠金利回り 29.48%) | SELL 2018-07-21 03:00:00 | 13.97% (証拠金利回り 41.90%) | BUY 2018-08-07 23:00:00 | 11.54% (証拠金利回り 07.50%) | SELL 2018-11-18 12:00:00 | 12.83% (証拠金利回り 22.58%) | SELL 2018-11-28 13:00:00 | 30.90% (証拠金利回り 40.17%) | SELL 2018-12-10 00:00:00 | 10.84% (証拠金利回り 06.07%) | SELL 2018-12-22 05:00:00 | 11.55% (証拠金利回り 17.55%) | BUY 2019-04-05 06:00:00 | 25.02% (証拠金利回り 43.54%) | BUY 2019-05-16 20:00:00 | 36.51% (証拠金利回り 52.93%) | BUY ------------------------------------------
どちらも同じ場面で(賭け金に対しては)同じリターンを得ていますが、証拠金に対する利回り(資金効率)がかなり違うのがわかると思います。
疑問に思うこと
良かった結果だけを見れば「複利で運用した方がいい」という結論になるのは明白です。 最初から絶対に勝てるとわかっているなら、複利で運用しない理由はありません。
しかし最終的な運用成績は、ある時点からある時点を切り取ったものにすぎないので、切り取る場所を変えれば結果もかわります。どの時点の成果をもって「結果が良かった」と判断するかは難しい問題です。実際にレンジ相場に突入したときにトレンドフォローBOTを止めたくなる理由もここにあります。
定率トレードの一番の問題は、今回のスイングトレンドフォローBOTのように、勝率が低くかつ売買頻度もそれほど多くない売買ロジックを使用した場合、複利で運用すると「大半の人は平均(期待値)通りのパフォーマンスを上げられず、最頻値や中央値はそれよりも低い方向に偏る」という点です。
これは最終資金が対数正規分布に近似するからで、詳しくは前回の記事(最終資金のモンテカルロシミュレーション)でも説明しました。定率トレード全般にいえることですが、BOTの勝率が低い場合により顕著にその影響が出ます。
簡単にいえば、一般的には複利の方がドローダウンのリスクが大きいということです。今回の結果でも最大ドローダウンは定率トレードの方が大きくなっています。そこで疑問なのは、ある場面で定額トレードと定率トレードのどちらの方が最善なのかを、トレード結果を元に何らかの指標で定量的に判断できるのだろうか?ということです。
モンテカルロシミュレーションで試すこと
ブートストラップ法(復元抽出)で最終資金をシミュレーションした場合に、定率トレードでどのくらい最終資金にバラつきが見られるかは、前回の記事で確認しました。なので今回は、同じく定額トレードのモンテカルロシミュレーションで最終資金の分布を確認して、その違いを比較してみたいと思います。
1.扱うサンプルの違い
前回の記事でも簡単に説明しましたが、定率トレードと定額トレードでは、復元抽出に使うリターンの種類が違います。
定率トレードでは、全てのリターンを初期資金に掛け合わせた結果が最終資金と一致しなければなりません。そのため、リターンの数字には「証拠金に対する利回り」を使います。一方、定額トレードでは、全てのリターンを固定額(100万円)に掛けて利益額を計算し、それを初期資金に足し合わせてシミュレーションします。そのため、リターンの数字には単に「賭け金に対するリターン」を使います。
▽ 定率トレードのリターンサンプル (148個)
-2.218,17.971,-2.265,-2.073,-2.095,-2.225,0.002,-2.203,-2.181,0.511,-2.169,29.482,-2.116,-2.169,-1.235,7.912,-2.137,-0.834,-2.243,-2.193,-2.239,-2.336,2.212,-2.296,-2.189,41.902,-2.243,-2.192,3.038,-2.177,7.502,5.834,-2.101,-1.265,-2.134,-2.099,-2.153,-2.184,-2.208,-2.19,9.222,2.963,6.776,-2.118,-2.172,-0.252,-2.23,2.162,-2.168,1.201,-2.236,-2.26,-2.18,1.385,-1.286,-1.889,-1.506,15.184,-2.224,-2.148,-2.14,-1.648,-1.133,-1.516,-1.373,-1.769,-1.596,-1.838,-1.379,-1.191,-2.069,-1.172,2.542,-1.082,-1.791,-1.022,22.584,40.172,-2.098,-2.055,-2.078,6.068,-2.141,4.268,17.553,-2.123,-2.063,-2.163,-2.272,-2.077,-2.225,-2.153,-2.432,-2.244,13.738,-2.228,-2.277,-2.09,-0.575,-2.136,-2.223,-2.312,8.391,-2.216,-2.348,-1.961,-1.374,-1.956,-1.642,-1.202,13.038,-2.27,0.825,-2.265,22.731,-2.189,0.167,-2.148,-2.271,0.616,-2.32,-2.075,-2.247,-2.206,2.374,-2.323,-0.613,-2.279,43.537,0.823,-0.199,-2.386,0.522,-2.265,-2.257,-2.103,-2.215,-2.21,-0.425,5.079,-2.262,-2.224,-2.278,7.367,-2.133,-2.185,52.935,-2.092
▽ 定額トレードのリターンサンプル (148個)
-1.155,11.162,-1.03,-3.291,-2.653,-1.264,0.001,-1.231,-1.464,0.549,-1.595,12.182,-2.405,-1.583,-1.817,4.976,-1.71,-1.667,-1.089,-1.329,-1.037,-0.797,0.945,-0.863,-1.53,13.967,-1.068,-1.282,4.747,-1.979,11.542,6.341,-2.693,-1.643,-2.667,-2.257,-1.619,-1.456,-1.636,-1.611,6.54,3.406,9.156,-1.78,-1.478,-0.153,-1.343,2.637,-1.436,0.765,-1.278,-0.991,-1.306,0.647,-0.429,-0.63,-0.502,5.061,-1.101,-2.237,-0.713,-0.551,-0.378,-0.505,-0.459,-0.592,-0.534,-0.613,-0.461,-0.397,-0.692,-0.392,0.85,-0.604,-0.597,-0.341,12.832,30.902,-3.179,-5.269,-3.406,10.836,-1.878,3.361,11.548,-2.498,-3.438,-1.545,-1.177,-2.967,-1.19,-1.538,-0.973,-1.24,4.61,-1.148,-0.994,-0.697,-0.756,-1.682,-1.101,-0.9,2.797,-1.185,-0.839,-0.654,-0.458,-0.652,-0.547,-0.401,6.179,-0.974,0.275,-0.913,9.316,-1.377,0.067,-0.716,-0.919,0.29,-0.951,-2.695,-0.994,-1.24,1.29,-0.821,-0.204,-0.904,25.021,0.799,-0.184,-0.907,0.45,-1.007,-1.016,-2.842,-1.231,-1.227,-0.196,2.04,-1.001,-1.917,-1.022,4.116,-1.839,-1.583,36.507,-4.981
2.定率トレードの最終資金のシミュレーション
定率トレードの場合の最終資金のモンテカルロシミュレーション(ブートストラップ法)については、すでに前回の記事で解説しているので、先に結果を見てしまいましょう。※注 定額トレードと比較の条件を揃えるために少しパラメータを変えたので、前回と結果は少し違っています。
トレード回数 148回
シミュレーション回数 50,000回
▽ 資産カーブ
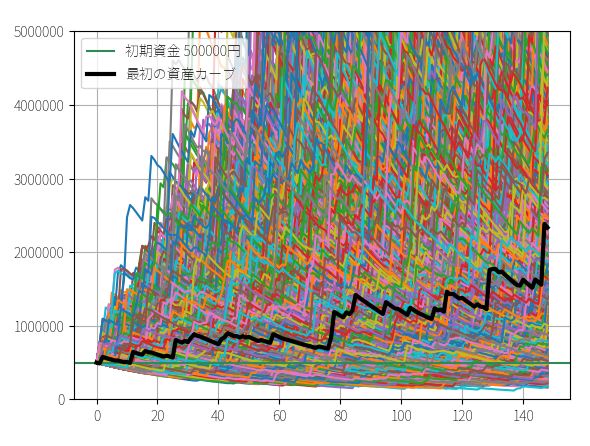
▽ 最終資金ヒストグラム(ビン数=1000)
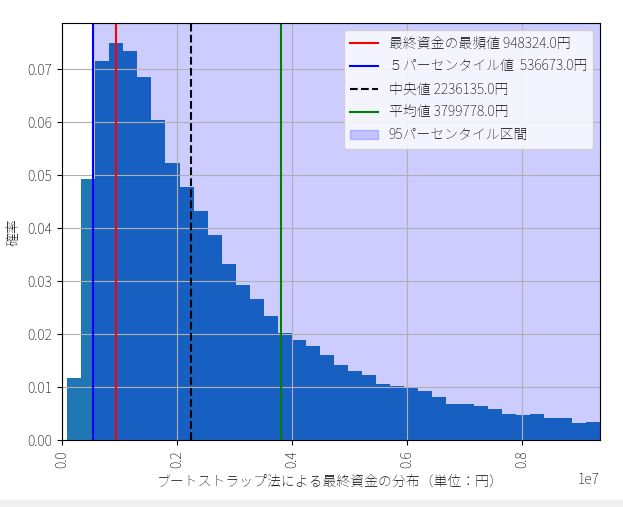
5%下位 53万6673円 (運用成績 107.3%)
最頻値 94万8324円 (運用成績 189.6%)
中央値 223万6135円 (運用成績 467.2%)
実際の成績 2332789円 (運用成績 466.5%)
ここで現実離れした右側の数値に意味があるわけではありません。正のリターンはサンプル数が少なくバラつきも大きすぎるからです。そのため、平均値が過大になっていますが、759%という数字が実際の市場で期待できる平均値という意味ではありません。ここでは1トレードあたりの勝率が低いことが原因で、最頻値が中央値よりかなり下方に偏っているという情報が重要です。
3.定額トレードの最終資金のシミュレーション
次に定額トレードの最終資金を、同じくブートストラップ法(サンプルの復元抽出)でシミュレーションします。
先ほども説明したように、定額トレードの場合は「賭け金に対するリターン」の数字からランダムにリサンプリングし、それを固定額(例:100万円)に掛け合わせた結果を初期資金に順番に足し合わせるプログラムを書きます。
▽ pythonコード
from matplotlib import pyplot as plt
import numpy as np
import scipy.stats as stats
import random
#------------------------------------
import matplotlib as mpl
font = {"family":"Noto Sans CJK JP"}
mpl.rc("font",**font)
#-------------------------------------
#----------------------------------------------------
# 準備
#----------------------------------------------------
data = np.genfromtxt("./return_fixed.csv",delimiter=",")
start_funds = 500000
trade_N = data.size
N = 50000
BET = 1000000
random_return = np.zeros((N,trade_N))
av_av_return = np.zeros(N)
# 資産推移の行列
asset_simulation = np.zeros((N+1,trade_N+1))
asset_simulation[:,0] = start_funds
for i in range(trade_N) : asset_simulation[0][1+i] = round(asset_simulation[0][i] + ((data[i]/100) * BET))
#----------------------------------------------------
# 使う関数
#----------------------------------------------------
# 勝率の計算
def winrate( data ):
r = np.sum( data>0 ) / data.size
r = round(r*100,1)
return r
# 平均リターンの計算
def av_return( data ):
r = data.mean()
r = round(r,2)
return r
# 勝ちの平均利益と負けの平均利益を計算
def win_lose_rate( data ):
win_r = np.where( data>0, data, 0 )
win_r = round( win_r.sum() / np.sum(data>0) ,2 )
lose_r = np.where( data<0, data, 0 )
lose_r = round( lose_r.sum() / np.sum(data<0) ,2 )
return win_r,lose_r
#----------------------------------------------------
# モンテカルロシミュレーション
#----------------------------------------------------
for i in range(N):
print("----------------------")
random_return[i] = np.array( random.choices( data, k=trade_N ) )
for k in range(trade_N) : asset_simulation[i+1][k+1] = round(asset_simulation[i+1][k] + ((random_return[i][k]/100)*BET) )
print("勝率 : {}% ".format( winrate(random_return[i]) ))
print("平均リターン : {}% ".format( av_return(random_return[i]) ))
win_r, lose_r = win_lose_rate( random_return[i] )
print("平均利益率 : {}% ".format( win_r ))
print("平均損失率 : {}% ".format( lose_r ))
av_av_return[i] = av_return(random_return[i])
#----------------------------------------------------
# リサンプリングで得られた平均リターンのヒスグラム
#----------------------------------------------------
n1,n2 = np.histogram( av_av_return, bins=50 )
average = round( av_av_return.mean(),2)
percentile_5 = np.percentile( av_av_return,5 )
percentile_95 = np.percentile( av_av_return,95 )
y = n1/float(n1.sum())
x = (n2[1:]+n2[:-1])/2
x_width = n2[1] - n2[0]
plt.bar( x, y, width=x_width )
plt.axvline( average, color="red", label="平均リターンの平均値 {}%".format(average) )
plt.axvspan( percentile_5, percentile_95, color="blue",alpha=0.1, label="95パーセンタイル区間")
plt.grid()
plt.xlabel("復元抽出した平均リターンの分布")
plt.ylabel("頻度")
plt.legend()
plt.show()
#----------------------------------------------------
# 資産カーブのグラフ化
#----------------------------------------------------
plt.grid()
for i in range(N): plt.plot( asset_simulation[i+1] )
plt.ylim(0,5000000)
plt.axhline( start_funds, color="#2e8b57", label="初期資金 {}円".format(start_funds) )
plt.plot( asset_simulation[0], color="black", lw=3, label="最初の資産カーブ" )
plt.legend()
plt.show()
#----------------------------------------------------
# 最終資金のヒストグラム
#----------------------------------------------------
last_funds = asset_simulation[:,-1]
median = np.median( last_funds )
average = round(last_funds.mean())
n1,n2 = np.histogram( last_funds, bins=1000 )
percentile_5 = np.percentile( last_funds,5 )
percentile_95 = np.percentile( last_funds,95 )
y = n1/float(n1.sum())
x = (n2[1:]+n2[:-1])/2
x_width = n2[1] - n2[0]
mode = round(x[np.argmax(y)])
plt.bar( x, y, width=x_width )
plt.axvline( mode, color="red", label="最終資金の最頻値 {}円".format(mode) )
plt.axvspan( percentile_5, percentile_95, color="blue",alpha=0.2, label="95パーセンタイル区間" )
plt.axvline( percentile_5, color="blue", label="5パーセンタイル値 {}円".format( round(percentile_5)) )
plt.axvline( median, color="black", linestyle="--",label="中央値 {}円".format(round(median)) )
plt.axvline( average, color="green", label="平均値 {}円".format(round(average)) )
plt.grid()
plt.xlabel("ブートストラップ法による最終資金の分布(単位:円)")
plt.ylabel("確率")
plt.xlim(0,last_funds[0]*4)
plt.xticks(rotation=90)
plt.legend()
plt.show()
実行結果
トレード回数 148回
シミュレーション回数 50,000回
▽ 資産カーブ
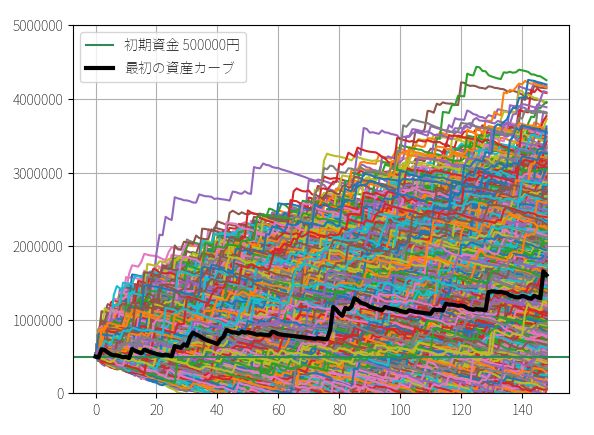
▽ 最終資金のヒストグラム(ビン数=1000)

定率トレードの結果に比べると歴然ですが、全く同じトレード機会にもかかわらず、定額トレードでは最頻値・中央値・平均値の3つがほとんど一致しています。いずれも150万円~160万円で、運に結果が左右される可能性が定率トレードに比べて低いことを意味しています。多数の人が、期待値とおりの成績を上げられる可能性が高いということです。
5%下位 55万7220円
最頻値 148万9661円
中央値 157万1390円
平均値 160万4651円
実際の成績 1602422円(320.0%)
ただし5%以下の運の悪さに遭遇したときの成績はほとんど同じです。0円まわり(破産確率)は定額トレードの方が高いくらいです。これは当たり前ですが、口座残高のn%を賭ける定率トレードは、数字上は破産しないからですね。定額トレードは、負けても賭け額を減らしたりしないので、正の期待値がなければ破産します。
どう判断するかを考える
定率トレードの最終資金の確率分布は対数正規分布に近づき、一方、定額トレードの最終資金の確率分布は正規分布に近づくことが理解できました。しかしこのグラフを眺めるだけだと、単に「定率トレードはリスクも大きいけどリターンも大きいよね」という、よく本に書かれている結論しか出てこず、結局どう意思決定すればいいのかわかりません。
今回のケースの場合、中央値は定率トレードの方が高いものの、最頻値は定額トレードの方が高いというヒントになりそうな有益な情報が得られました。ということは、最初の疑問に答えるためには、「最頻値」と「中央値」のどちらを信じてトレードするべきか?という問題が鍵になりそうです。
「最頻値と中央値のどちらを信じて意思決定するべきか?」という質問に、教科書的な答えはあるのでしょうか?
1.統計的な意思決定
私も詳しくありませんが、統計学の世界ではこのように「確率分布の中からどれか1つだけ代表値を選ばなければならない場面での意思決定の方法」についての学問分野があり、それを統計的意思決定というそうです。
結局のところ、「目的に応じて最適な数字を選ぶしかない」というありきたりな結論になるのですが、せめてそれを関数にして最適解を求めようということです。このような関数を損失関数というそうです。よくファイナンスの用語で損失関数という言葉を聞きますが、そういう意味なんですね。(参考:「pythonで体験するベイズ推論」5章より)
例えば、以下のような指標を作って定量的に判断します。
(漠然とした気持ち)
「定率トレードの方が大きく儲かる可能性が高いなら、多少のリスクを背負っても定率トレードにしたいなぁ。でも固定額トレードの平均を下回るのは悔しいよな...。その可能性の方が高いならやめておこうかなぁ...。」
(統計的意思決定)
原則として定率トレードを選択する。ただし定率トレードの最終資金が定額トレードの期待値を下回る確率が50%を超えるなら定率トレードはやめる。
2.損失関数をつくろう
モンテカルロシミュレーションの素晴らしいところは、数十万回のトレード結果の事後分布を得られるので、上記の確率を実際に計算できることです。さっそく「最終資金が定額トレードの平均を下回る確率が50%を超える」かどうかを判定する損失関数を作りましょう。
#----------------------------------------------------
# 意思決定するための損失関数
#----------------------------------------------------
def judgment( last_funds ):
probability = np.array( last_funds<1600000 ).mean()
print("--------------------------")
print("推測される確率 : " ,probability)
print("--------------------------")
if probability > 0.5:
print("定額トレードを選択すべき")
else:
print("定率トレードを選択すべき")
これだけでOKです。めちゃくちゃ簡単です。
変数 last_funds には、モンテカルロシミュレーションで得られた10万回分の最終資金の結果がリスト形式で保存されています。それを以下のコードによって、定額トレードの平均(160万円)を下回っているかどうかで True/false の二値の配列に変換します。
np.array( last_funds < 定額トレードの平均値 )
真偽値のTrueは1、Falseは0なので、そのリストの平均を取れば、Trueの確率(全ての最終資金のうち160万円を下回った結果の割合)を計算できます。
このようにモンテカルロシミュレーションで得られた大量のサンプルから、ある条件に当てはまるかどうかを True/False の二値変数に変換して、Trueの割合から確率を推測する方法は、ベイズ推計(事後確率)の基本的な考え方のようです。さきほど紹介した書籍のほか、本「基礎からのベイズ統計学」6章などでも紹介されています。
実行結果
定率トレードの結果が、定額トレードの平均的な結果を下回る確率は約36%であり、最初に立てた意思決定の基準に照らし合わせると定率トレードを選択することが合理的である、とわかります。
注意点
このようにモンテカルロシミュレーションの優れた点は、実際に意思決定するときに必要となる基準点の確率をちゃんと計算できる点にあります。以下のグラフでいうと、最終資金が160万円を下回る確率が35%だとわかる、ということです。

ただしこのような意思決定を行う場合には、結果を見る前に意思決定の基準を決めて、それを守ることが大事です。売買ロジックの評価と全く同様で、損失関数のパラメータ(ここでは160万円と50%という数字)も自由度の1つなので、ずるずると弄るといくらでも望むような結果を出せてしまいます。
例えば、最初から「本当は定率トレードでやりたい..」という思い込みがあり、上記の結果を見たあとに、もし悪かったら「じゃあ100万円を下回る確率ならどうだろう..」「じゃあ40%以上ならどうだろう?」と結果を見ながら数字を変更しはじめると、損失関数を使うことに何の意味もないということです。
おお、久しぶりにのぞいたら更新されていてびっくりしました。
このサイトをきっかけに自分でも1年ちょっと自動売買を続けてきましたが、(今はpythonやEA等)今見返しても内容が濃くて参考になります。
これからも時たま更新があれば読まさせていただきます!
PS.去年は流行りすぎてドテン狩り?などまで出始めてあまり優位性は無くなったみたいな感じでしたが、ドンチャンも期間によってはずっと機能し続けてましたね。(具体的には期間40台とか?今はどうかわかりませんが・・・)奥が深いなぁ汗
このサイトは一つの手法に対してのアプローチも色々でそういう面でもとても勉強になります。
コメントありがとうございます
全然更新できていないですが、1年振りに来てくださって嬉しいです。
8月に調べた時点では、1年スパンなら期間20~50はどれでも(レンジ相場で止めてさえいなければ)利益が出ていたのではないかと思います。ただ結果論なので、どのパラメータでどの程度の利益がどの程度のスパンで出るかを将来について事前に予測することはほぼ不可能に近い気がしますね。
おっしゃる通り、ドンチャンは一番シンプルな売買ルールなのに、それすらどういう条件が揃えば利益が出るのか正確に理解するのは困難で、私もトレードは奥が深いなと感じていますw はい、またぜひ来てください!