さて、前回の3記事で「破産確率の公式」については理解できたと思います!長かったので読むのが大変だったと思います。お疲れ様でした。
破産確率の公式を理解するにはどうしても数学が必要です。ここを面倒だからと飛ばそうとすると、つい何を計算しているのかわからないまま「破産確率は1%を超えてはいけない!」などの数値目標だけを鵜呑みにしがちになります。
そのため少し難しい内容でしたが、敢えて本編で丁寧に解説させていただきました。
1.高校数学で正しいFXの破産確率を理解しよう(1)
2.高校数学で正しいFXの破産確率を理解しよう(2)
3.高校数学で正しいFXの破産確率を理解しよう(3)
今回の記事では、いよいよ自作BOTの破産確率(ドローダウン発生率)を計算し、それを口座リスク別に集計して「実用的な破産確率表」を作成する方法を紹介します!
1.実用的な破産確率表の作り方
すでに説明したように、破産確率を計算するためには以下の情報が必要です。
1)損益レシオ
2)勝率
3)口座のリスク率
4)初期資金
5)撤退ライン(破産ライン)
破産確率表というと、一般的には、損益レシオと勝率で表にすることが多いです。しかしこれらの数字は、売買ロジックの検証の時点ですでに決定されています。
勝率や損益レシオの数値は、トレーダーの意思で自由に調整できる数字ではないので、表にしても具体的な意思決定にはあまり役に立ちません。「期待値は高ければ高いほどいい」という当たり前の事実を確認するだけで終わってしまいます。
△ 破産確率は後者の意思決定に関する問題
本来、期待値が0円を超えていれば、破産確率は単に資金管理上の問題にすぎないことを思い出してください。期待値がプラスの場合、ロット数を十分に下げれば破産することは絶対にありません。
そのため、ここでは「すでに損益レシオと勝率がわかっているBOT」を運用する際に「口座のリスク率を決定する」ための判断材料として、破産確率表を使うことを想定します。
具体的には、縦(行)に口座のリスク率(X%)、横(列)にドローダウン率(Y%)をとり、特定のドローダウンが生じる確率(=破産確率)を示した表を作ります。
2.損益レシオを計算するコード
損益レシオを計算するコードだけ、まだ過去記事では作ったことがなかったので、一応、作り方を紹介しておきます。やり方は、pandasの記事で紹介しています。
▽ 損益レシオの計算コード
# バックテストの集計用の関数
def backtest(flag):
print("バックテストの結果")
print("-----------------------------------")
print("平均利益率 : {}%".format(round(records[records.Profit>0].Rate.mean(),2)))
print("平均損失率 : {}%".format(round(records[records.Profit<0].Rate.mean(),2)))
print("損益レシオ : {}".format(round( records[records.Profit>0].Rate.mean()/abs(records[records.Profit<0].Rate.mean()) ,2)))
試しに、前回の章で作ったドンチャン・チャネルブレイクアウトBOTの平均利益率と損益レシオを確認しておきましょう。
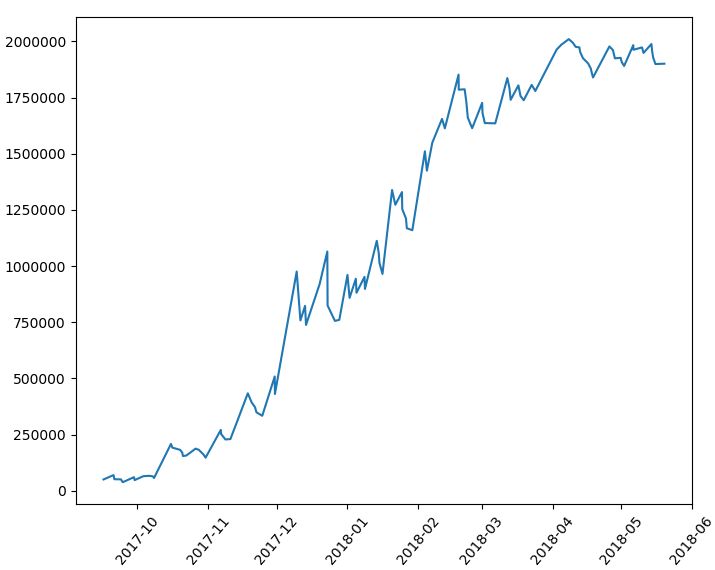
・1時間足を使用(2017/8~2018/5)
・上値ブレイクアウト判定期間 30期間
・下値ブレイクアウト判定期間 30期間
・平均ボラティリティ計算期間 30期間
・ブレイクアウトの判定基準(高値/安値)
・損切りレンジ 2ATR
----------------------------------- 総合の成績 ----------------------------------- 全トレード数 : 111回 勝率 : 38.7% 平均リターン : 1.7% 平均利益率 : 9.39% 平均損失率 : -3.16% 損益レシオ : 2.97 平均保有期間 : 45.0足分 損切りの回数 : 54回
なお、この破産確率の計算の元となる「損益レシオ」の計算には、分割エントリー(増し玉)を使わないように注意してください。
ポジションの積み増しを有りでシミュレーションすると、勝率や平均利益率などが歪むため、正しい破産確率を計算できなくなります。詳しくは分割エントリーの記事を参考にしてください。
3.破産確率表を作るコード
破産確率表を作るコードは、前回の記事の「破産確率を計算するコード」を応用して作成します。まずは最初にコードを確認しておきましょう。
import numpy as np
import pandas as pd
from datetime import datetime
# 設定値
winning_percentage = 0.387 # 勝率
payoff_ratio = 2.97 # 損益レシオ
funds = 1000000 # 初期資金
drawdown_rate_list = np.arange(10,100,10) # ドローダウン率 10~90%の配列
risk_rate_list = np.arange(0.5,10,0.5) # 口座のリスク率 0.5~9.5%の配列
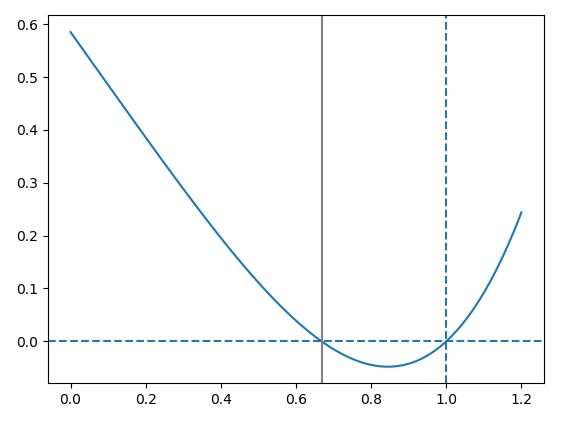
# 特性方程式の関数
def equation(x):
k = payoff_ratio
p = winning_percentage
return p * x**(k+1) + (1-p) - x
# 特定方程式の解を探す
def solve_equation():
R = 0
while equation(R) > 0:
R += 1e-4
if R>=1:
print("期待値が0を下回っています")
R=1
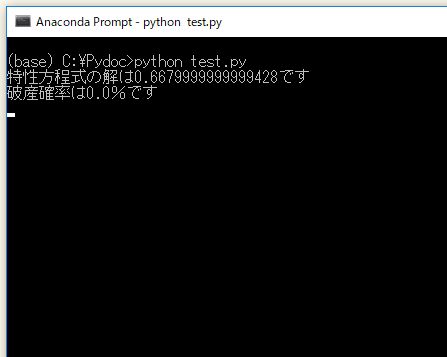
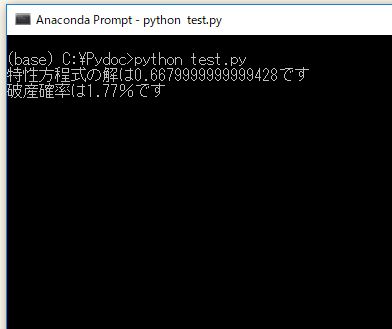
print("特性方程式の解は{}です".format(R))
return R
# 破産確率を計算する公式
def calculate_ruin_rate( R, risk_rate, drawdown_rate ):
bankrupt_line = int(round(funds * (1 - drawdown_rate / 100)))
risk_rate = risk_rate / 100
print("破産ライン : {}円".format(bankrupt_line))
unit = (np.log(funds) - np.log(bankrupt_line)) / abs(np.log( 1-risk_rate ))
unit = int(np.floor(unit))
return R ** unit
# メイン処理
result = []
for risk_rate in risk_rate_list:
temp = []
for drawdown_rate in drawdown_rate_list:
print("口座のリスク率:{}%".format(risk_rate))
print("ドローダウン率:{}%".format(drawdown_rate))
R = solve_equation()
ruin_rate = calculate_ruin_rate(R,risk_rate,drawdown_rate)
ruin_rate = round(ruin_rate * 100,2)
print("破産確率は{}%です".format( ruin_rate ))
temp.append(ruin_rate)
print("------------------------------------------")
result.append(temp)
# pandasで表に集計する
df = pd.DataFrame(result)
df.index = [str(i)+"%" for i in risk_rate_list]
df.columns = [str(i)+"%" for i in drawdown_rate_list]
print(df)
# 最終結果をcsvファイルに出力
df.to_csv("RuinTable-{}.csv".format(datetime.now().strftime("%Y-%m-%d-%H-%M")) )
縦(行)に口座のリスク率を0.5%刻みで配列にし、横(列)にドローダウン率を10%刻みで配列にします。基本的な手順は、以前にバックテスト編で解説した「for文の総当たり探索の方法」と同じです。
・参考記事
for文での総当たりで最適なパラメーターを探索する方法
それでは実行結果を確認しておきましょう!
実行結果
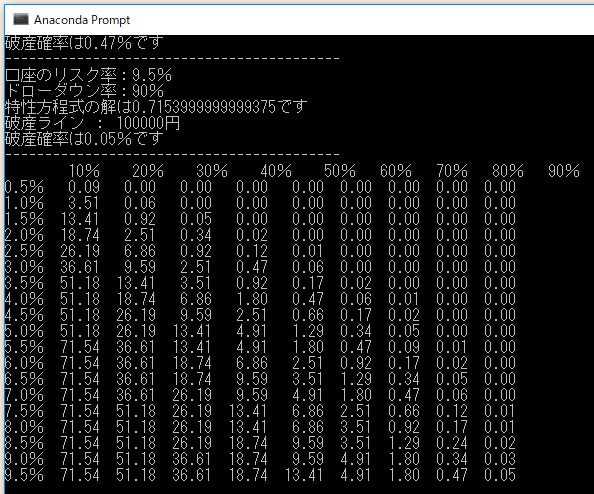
以下のようなCSVファイルが出力されます。
検証結果
上記のチャネルブレイクアウトBOTの破産確率表(ドローダウンの発生確率表)は以下のようになりました。この表は左の「口座のリスク率」を取った場合に、右の「ドローダウン率」がおこる確率を示しています。
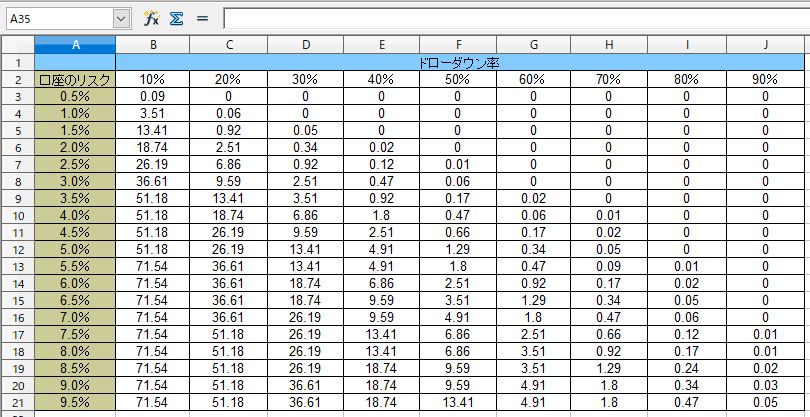
このBOTはそれなりにバックテスト上の成績がいいため、口座資金が0円になるという意味での「破産確率」はほとんどありません。
しかし例えば、このBOTを「口座のリスク5%」で運用した場合、13%の確率で30%以上のドローダウンに見舞われ、1.2%の確率で50%以上のドローダウンに見舞われることになります。それが許容できる確率であれば、5%での運用は十分に選択肢に入ります。
一方、50%のドローダウンがおこる確率(破産確率)を完全に0%におさえたいなら、口座のリスク率は2%で運用するのが適切ということになります。
確率の考え方の注意点
「5%以上の確率」は実現する可能性があると覚悟しておいた方がいいでしょう。絶対におこって欲しくない水準のドローダウン確率は、1~2%以下になるように、口座のリスク率を設定しましょう。
また上記の破産確率表は、あくまで過去のバックテスト上の「勝率」「損益レシオ」を将来にも再現できた場合の破産確率である点に注意してください。もし勝率や損益レシオが悪化すれば、この表よりも実際の破産確率は高くなります。
またここで使った勝率や損益レシオはあくまで「平均値」であることも忘れないでください。月単位などの局所的なドローダウン発生率にはもっとバラつきがあるため、余裕を持ってリスク率を決めてください。
途中時点での再計算
また「破産確率は資金量の関数である」ことを忘れないようにしましょう。資金の量が変われば破産確率は常に変動します。
例えば、口座リスク5%で運用した場合、上記の表では100万円の時点で資金が50万円にまで減る確率(50%のドローダウンがおこるリスク)は1.3%しかありません。しかし資金が70万円まで目減りした時点での「資金が50万円にまで減る確率」は13%と飛躍的に高くなります。
▽ 初期資金からのドローダウン確率を、資金70万円(-30%)の時点で再計算した場合
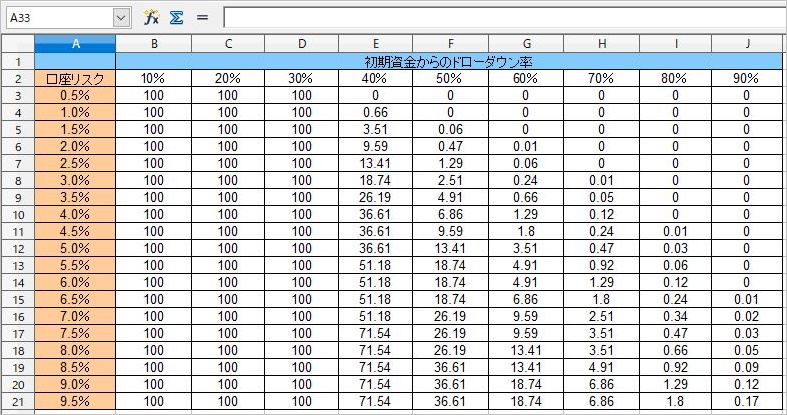
そのため、「初期資金を絶対に50%以下に減らしたくない」のであれば、資金が70万円まで減った時点で「口座のリスク率」を2.5%以下に再調整しなければなりません。
繰り返しますが、破産確率(ドローダウン確率)は資金量の関数です。そのため、常に破産確率を一定水準以下におさえるためには、資金が減るたびに破産確率を再計算して、それに合わせて口座のリスク率を引き下げる必要があります。
興味がある方は、現在の証拠金残高と許容できるドローダウン率から、注文前に自動的に「口座リスク率」を再計算して調整するようなBOTを作ってもいいでしょう。
練習問題
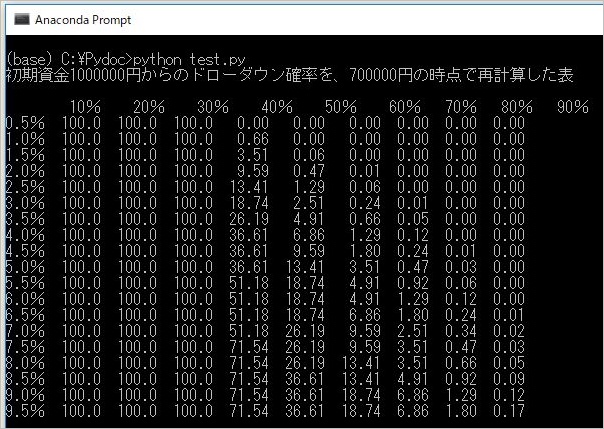
本文の途中に出てきた、「初期資金からのドローダウンが生じる確率を途中資金の時点で再計算した場合」の破産確率表のコードを作ってみましょう! 以下にそのまま正解例のコードを記載しておきます。
import numpy as np
import pandas as pd
from datetime import datetime
# 設定値
winning_percentage = 0.387 # 勝率
payoff_ratio = 2.97 # 損益レシオ
funds = 1000000 # 初期資金
funds2 = 700000 # 途中経過時点での資金
drawdown_rate_list = np.arange(10,100,10) # ドローダウン率 10~90%
risk_rate_list = np.arange(0.5,10,0.5) # 口座のリスク率 0.5~9.5%
# 特性方程式の関数
def equation(x):
k = payoff_ratio
p = winning_percentage
return p * x**(k+1) + (1-p) - x
# 特定方程式の解を探す
def solve_equation():
R = 0
while equation(R) > 0:
R += 1e-4
if R>=1:
R=1
return R
# 破産確率を計算する公式
def calculate_ruin_rate( R, risk_rate, bankrupt_line ):
risk_rate = risk_rate / 100
unit = (np.log(funds2) - np.log(bankrupt_line)) / abs(np.log( 1-risk_rate ))
unit = int(np.floor(unit))
return R ** unit
# メイン処理
result = []
bankrupt_line_list = []
for drawdown_rate in drawdown_rate_list:
bankrupt_line_list.append(int(round(funds * (1 - drawdown_rate / 100))))
for risk_rate in risk_rate_list:
temp = []
for bankrupt_line in bankrupt_line_list:
R = solve_equation()
ruin_rate = calculate_ruin_rate(R,risk_rate,bankrupt_line)
ruin_rate = round(ruin_rate * 100,2)
if ruin_rate > 100:
ruin_rate = 100.0
temp.append(ruin_rate)
result.append(temp)
df = pd.DataFrame(result)
df.index = [str(i)+"%" for i in risk_rate_list]
df.columns = [str(i)+"%" for i in drawdown_rate_list]
print("初期資金{}円からのドローダウン確率を、{}円の時点で再計算した表\n".format(funds,funds2))
print(df)
# 最終結果をcsvファイルに出力
df.to_csv("RuinTable-{}.csv".format(datetime.now().strftime("%Y-%m-%d-%H-%M")) )